Buoyancy:
When a body is immersed in fluid an upward force is exerted by the fluid on the body. This upward force is equal to the weight of the fluid displaced by the body is called the force of buoyancy or buoyancy.
Center of Buoyancy:
It is defined as the point through which the force of buoyancy is supposed to act. As the force of buoyancy is a vertical force and is equal to the weight of the fluid displaced by the body the center of buoyancy will be the center of gravity of the fluid displaced.
Floating concept:
When any boat displaces a weight of water equal to its own weight, it floats. This is often called the “principle of floatation”, a floating object displaces a weight of fluid equal to its own weight. Every ship, submarine must be designed to displaced weight of fluid at least equal to its own weight.
Condition of equilibrium: Stability of submerged and floating body
A submerged or a floating body is said to be stable if it comes back to its original position after a slight disturbance.
Stability of a submerged body:
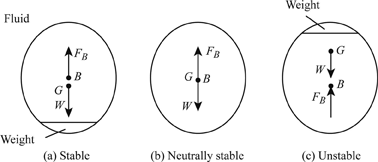
The position of center of gravity and center of buoyancy in case of completely submerged body are fixed. Consider a balloon which is completely submerged in air. Let, the lower portion of balloon contains heavier material so that its center of gravity is lower than its center of buoyancy as shown in figure a. Let, the weight of the balloon is W. The weight W is acting through G vertically in the downward direction while the buoyant force FB is acting vertically up, through B. For the equilibrium of the balloon W= FB. If the balloon is given an angular displacement in the clockwise direction as shown in figure a, then W and FB constitute a couple acting in the anti- clockwise direction and brings the balloons in the original position. Thus the balloon in the position shown in figure a is in stable equilibrium.
- Stable Equilibrium :
When W =FB and center of buoyancy (B) is above center of gravity (G), the body is said to be in stable equilibrium.
- Unstable Equilibrium:
If W= FB, but the center of buoyancy (B) is below center of gravity (G) the body is in unstable equilibrium as shown in figure b. A slight displacement to the body in the clockwise direction gives the couple due to W and FB also in the clockwise direction. Thus the body does not return to its original position and return to its original position and hence the body is in unstable equilibrium.
- Neutral Equilibrium:
If FB =W and center of buoyancy (B) and center of gravity (G) are at the same point as shown in figure c the body is said to be in neutral equilibrium.
Stability of floating body:
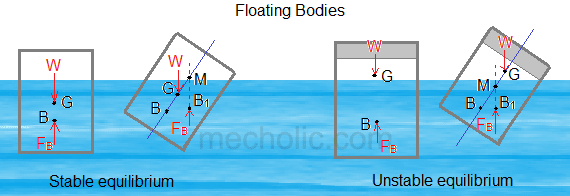
The stability of a floating body is determined from the position of metacenter (M). In case of floating body the weight of the body is equal to the weight of liquid displaced.
- Stable Equilibrium:
If the point M is above G, the floating body will be stable equilibrium as shown in figure a. If a slight angular displacement is given to the floating body in the clockwise direction the center of buoyancy shifts from B to B1such that the vertical line through B1 cuts at M. Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anticlockwise direction and thus bringing the floating body in the original position.
- Unstable Equilibrium:
If the point M is below G, the floating body will be in unstable equilibrium as shown in figure B. The disturbing couple is acting in the clockwise direction. The couple due to buoyant force FB and W is also acting in the clockwise direction and thus overturning the floating body.
- Neutral Equilibrium:
If the point M is at the center of gravity of the body, the floating body will be in neutral equilibrium.
Summary:
| Submerged Body | Floating Body |
| Stable: Center of gravity below center of buoyancy. | Stable: Center of gravity below metacenter |
| Unstable: Center of gravity above center of buoyancy. | Unstable: Center of gravity above metacenter |
| Neutral: Center of gravity coincides with center of buoyancy. | Neutral: Center of gravity lies at metacenter. |
Metacenter and determination of metacenter height (Experimental and Analytical Method)
Metacenter:
Metacenter is defined as the point at which the line of action of the force of buoyancy will meet the normal axis of the body when the body is given a small angular displacement.
Metacentric Height:
The distance between the metacenter of a floating body and the center of a floating body and the center of gravity of the body is called metacentric height.
Experimental Method for determination of metacentric height:
Let,
W= Weight of vessel including w1
G = Center of gravity of the vessel
B = Center of buoyancy of the vessel
The weight w1 is moved across the vessel towards right through a distance x as shown in figure B. The vessel will be tilted. The angle of heel θ is measured by means of a plumbline and a protractor attached on the vessel.The new center of gravity of the vessel will be G1 as the weight w1 has been moved toward the right.
Above the center of buoyancy will change to B1 as the vessel has tilted.
Under equilibrium the moment caused by the movement of load w1 through a distance x must be equal to the movement caused by the shift of center of gravity from G to G1 .
Thus,
The moment due to change of G
= GG1 * W
= W * GMtanθ
The moment due to movement of w1
= w1 * x
From above equation,
w1 * x = W * GMtanθ
or, GM = (w1 * x)/ Wtanθ
Analytical Method for Metacentric height:
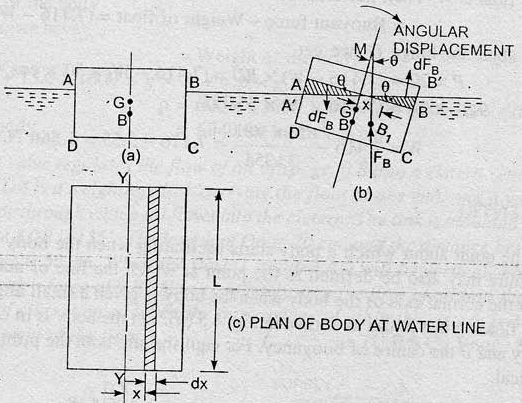
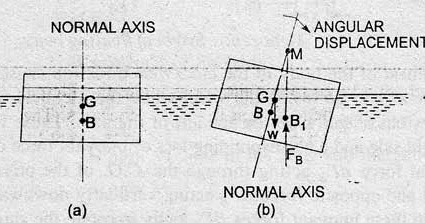
In figure A, it shows the position of a floating body in equilibrium. The location of center of gravity and center buoyancy in this position is at G and B. The floating body is given a small angular displacement in the clockwise direction. This is shown in figure B. The new center of buoyancy is B1. The vertical line through B1 cuts the normal axis at M. Hence, M is the metacenter and GM is metacentric height.
Couple due to wedges
Consider towards the right of the axis a small strip of thickness dx at a distance x from O as shown in figure B.
The height of strip x ∠ BOB’ = x* θ [∴∠BOB’ = ∠AOA’ = ∠BMB1’=θ]
∴Area of strip = Height * Thickness
= x* θ*dx
If L is the length of the flaoting body,then
Volume of strip = Area * L
= x* θ*L*dx
∴Weight of strip = ρg*Volume
= ρg *x* θ*L*dx
Moment of the couple = Weight of each strip * Distance between these weigth
= ρg x θLdx*[x+x]
= 2ρg x2 θLdx
∴Moment of couple for the whole wedge=∫2ρg x2 θLdx ——(i)
Moment of couple due to shifting of center of buoyancy from B to B1
= FB * BB1
= FB * BM* θ [∴ BB1 = BM* θ , if θ is very small]
= W * BM* θ [∴ FB = W] ————(ii)
Hence,equating equation (i) and (ii)
W * BM* θ =∫2ρg x2 θLdx
Or, W * BM* θ = 2ρgθ∫ x2 Ldx
Or, W * BM = 2ρg∫ x2 Ldx
But,
Ldx = dA [∴ Elemental area on the water line shown in figure C]
∴W*BM=2ρg∫ x2 dA
But, figure C it is clear that 2∫ x2 dA is the second moment of area of the plane of the body at water surface about the axis Y-Y.
Therefore,
W*BM = ρgI [∴ where I = 2∫ x2 dA]
∴ BM = (ρgI)/ W
But,
W= Weight of the body
= ρg * Volume of the body submerged in water
= ρg * ∀
∴ BM = (ρgI)/ ρg * ∀
Or, BM = I/∀
Now,
GM = BM – BG
= (I/∀) – BG
∴Metacentric height = GM = (I/∀) – BG
References: 1. A text book of fluid mechanics and hydraulic machines, Dr. RK Bansal, (2008), Laxmi publication(P) LTD.