Strain Energy Method: due to axial stress, bending, torsion, shear

Strain energy and Complementary Strain Energy

• When an elastic member is deformed under the action of an external loading the member is said to have possessed or stored energy which is called strain energy.
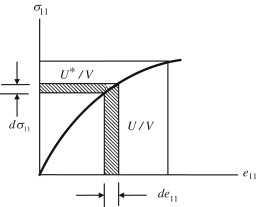
• The strain energy stored by a member so deformed is equal to the amount of work done by the external forces to produce deformation.
• The area between the load-extension curve and the vertical axis is called complementary energy.
• For linearly elastic materials this area is equal to the area under the load extension curve i.e. strain energy.

Strain Energy Due To Bending

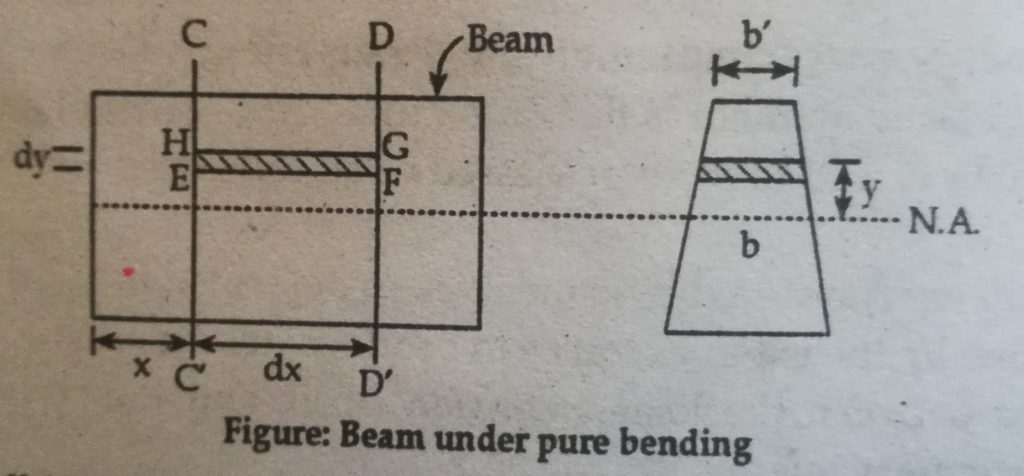
Consider a small length dx of a beam where the bending moment is M. Consider further a small strain EFGH of thickness dy at a distance y from the neutral axis.

Let,

Width of strip = b

Volume of strip = d_X *d_y * b

We have,

Strain energy in element (dU) = ½ * Stress * Strain * dV

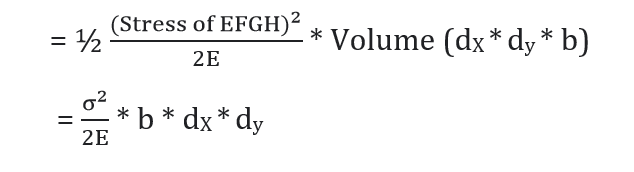
Also, from flexural formula,

σ = (M/I)*y

Then,

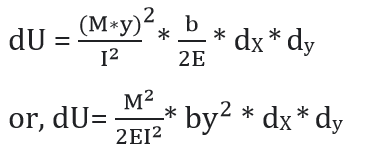
∴ dU = Strain energy of the volume CC’D’D

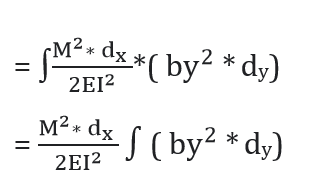
Now,

∫by²*d_y = Sum of second moment of area b.d_y

                 = Moment of inertia of beam cross-section

                 = I

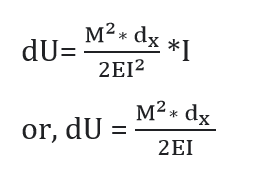
The above expression gives the strain energy of the beam of length d_x .

Hence, Strain energy of the whole of the beam is given by;

If M is constant over the length L. Then,

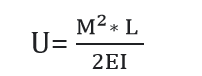
Strain Energy Due To Torsion

We know that,

Elemental strain energy (dU)= ½ *stress* strain *dV

Where,

𝜏 = Maximum shear stress on the surface of the shaft.

G= Modulus of rigidity

Where,

T= Torque applied

 J =  Polar moment of inertia

L = Twisting angle

Φ = Twisting angle

Now,

The above expression is the required expression.

Strain Energy Due To Shear

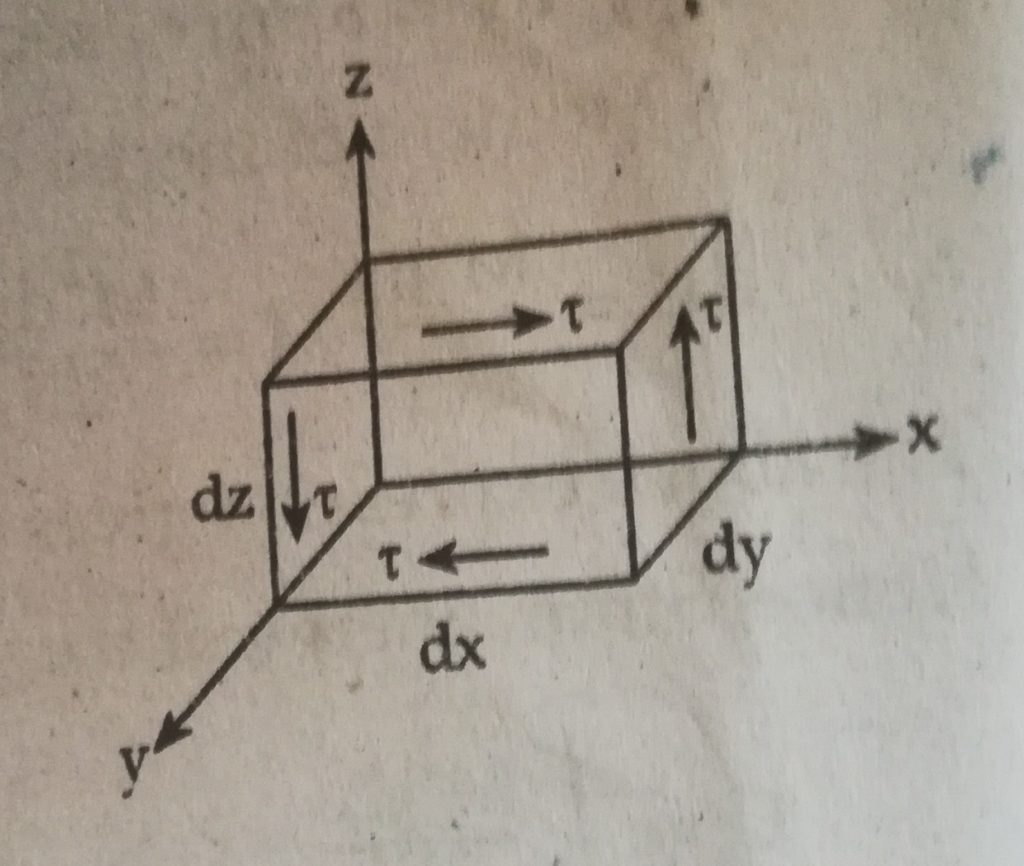
Let the infinitesimal element is under the system of shear stress (𝜏) as shown in figure.

Now,

Strain energy stored in element ( dU) = ½ * stress * strain* dV

Or, dU = ½ * 𝜏 * γ * dV

Where,

𝜏 = Shear stress

γ = Shear strain

Also,

Modulus of rigidity (G) = 𝜏 / γ

Or,  γ = 𝜏 / G

Putting the value in above expression; we get

dU = ½ *𝜏 * 𝜏 / γ *dV

Case I : Shear stress on rectangular beam,

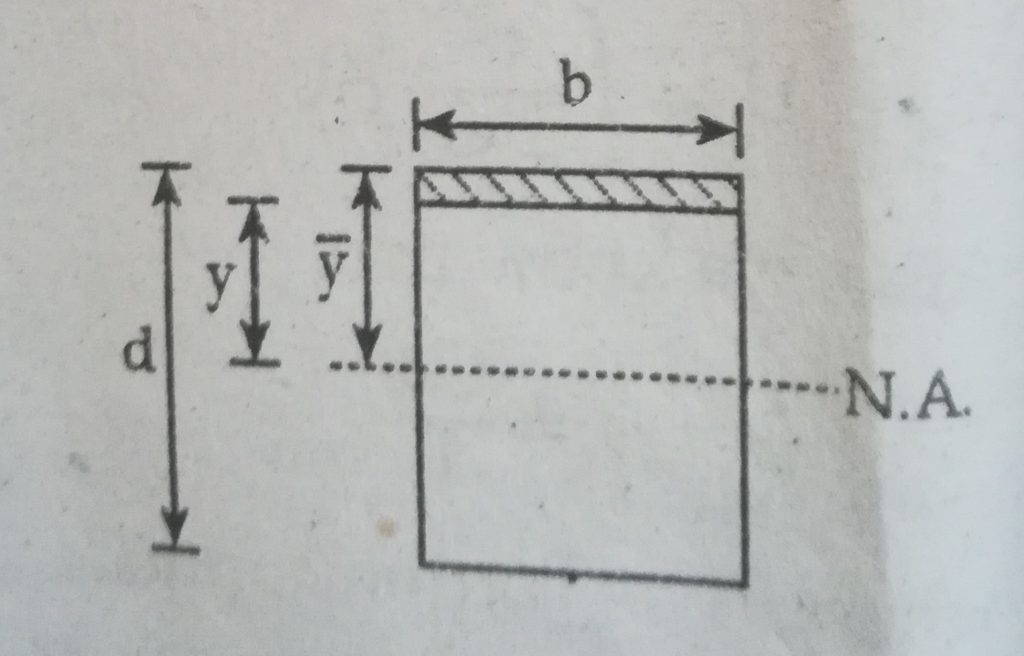
We have,

Shear stress (𝜏) = (VA y̅) / I*b ————-(2)

Where,

V= Shear force

A= Area above considered strip

y̅ = Center of gravity of area above considered strip

b= Width of beam

d= Depth of beam

I = Moment of inertia about direction of V

Now,

Shaded Area (A) = b(d/2 – y)

And

y̅ = ½ ( d/2 + y)

or, A y̅ = b/2 (d² /4 – y² )

From equation (1) and (2) ; we have

U= ∫ dU

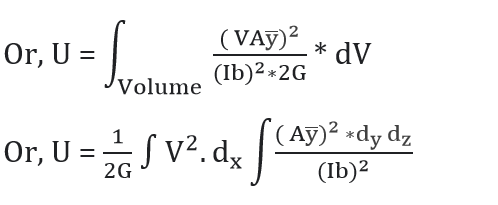
Put Ay̅ = Q = Static moment of the cross- sectional area, above the point where the shear stress is desired.

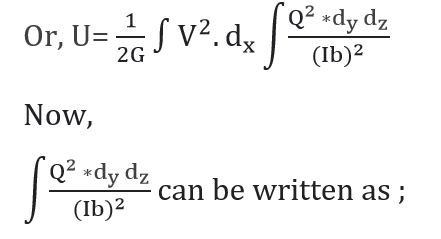
Hence,

Rectangular section A_s = bd/1.2

This factor is known as shape factor whose value is dependent on actual shear stress distribution over the cross section.

Case II: Shear stress on circular beam

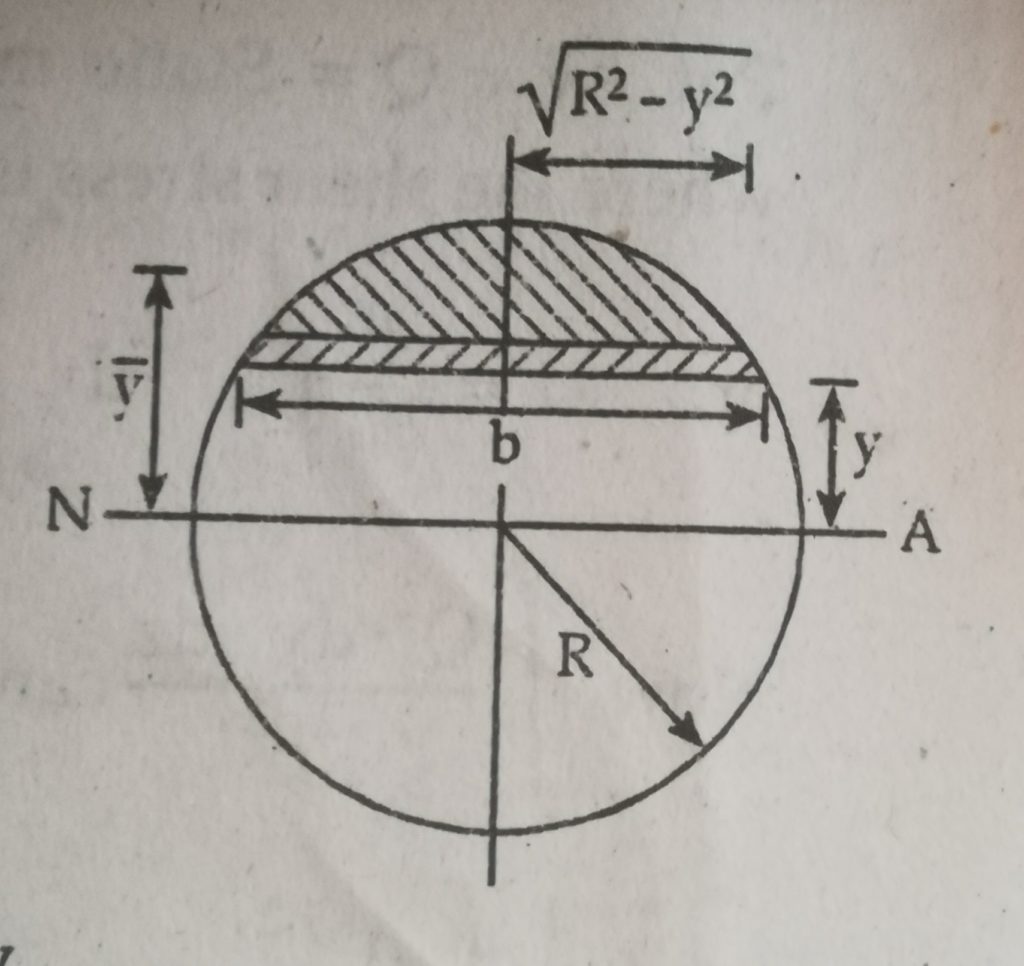
Consider a solid circular section of radius R and an elementary strain of thickness dy at a distance y from N.A. Let the width of strip be b.

Then,

b=2(R² – y²)^1/2

Area of elementary strip (dA) = b*dy

                                                          = 2(R² – y²)^1/2 *dy

Moment of elementary area about N.A

 = dy *y = 2(R² – y²)^1/2 *y*dy

For shaded area;

We have,