Study of rock mass classification system

Rock Mass Classification

Rock mass: The large volume of rock intersected by discontinuities is known as rock
mass.
The rock mass is heterogeneous in nature due to variation in rock type,
discontinuities and degree of weathering.
Rock mass = Intact rock + Discontinuities
The discontinuities highly influence the overall strength of rock mass.

Strength of rock mass < Intact rock

Intact rock:

The intact rock is the rock in which there is absence of discontinuities.

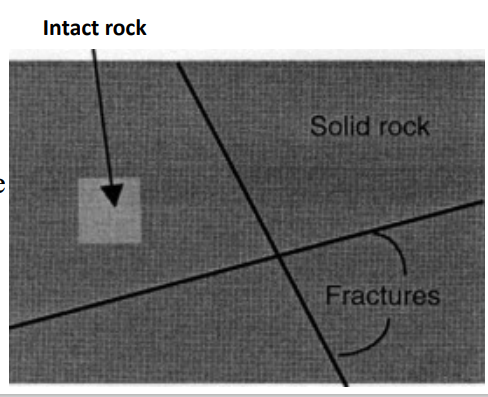
Discontinuities:

Discontinuities are the structural features of rock which are developed due to existence of different stress on the periphery of the earth. Discontinuities includes bedding plane, joints or fracture etc.

Properties of Discontinuities

The properties of discontinuities are:
a) Orientation
b) Spacing
c) Continuity (persistence)
d) Aperture (width) and Infilling
materials
e) Surface Characteristic
(Roughness)
f) Groundwater condition

Rock mass classification system

Different rock mass classification system has been established till now by different researcher. The
rock mass classification helps to improve the quality of site investigation by providing quantitative
information for design purpose. It is also used to determine the strength of rock and help to
determine the support condition required for rock to provide designed strength and leads to
successful completion of project.

Different rock mass classification systems are as follows:
a) Terzaghi’s rock mass classification system
b) Rock quality designation index (RQD)
c) Rock mass rating system (RMR)/ Bieniawski’s/ Geomechanical classification System
d) Rock tunneling quality index ( Q- value)

a) Terzaghi’s rock mass classification

This is the first organized rock mass classification system proposed by
Dr. Karl Terzaghi (1946). The system was mainly qualitative and used
for rock tunnel design and construction projects.
• Intact rock: Rock with no joints and hair cracks.
• Stratified rock: Rock with little strength along bedding surface.
• Moderately jointed rock: Rock mass jointed but cemented.
• Blocky and seamy rock: Jointed rock mass without any cementing of
joints.
• Crushing rock: Rock that has been reduced to sand size particles
without any chemical weathering.
• Squeezing rock: Rock containing considerable amount of clay.
• Swelling rock: Rock that squeezes primarily from mineral swelling.

b) Rock Quality Designation Index

The Rock Quality Designation index (RQD)
was developed by Deere (Deere et al 1967) to
provide a quantitative estimate of rock mass
quality from drill core logs. RQD is defined as
the percentage of intact core pieces longer than
100 mm (4 inches) in the total length of core.

Sometime the drilling core is not available in such case the RQD can
be determined by the relation suggested by Plamstrom as shows
below:
RQD = 115 – 3.3 Jv
Where,
Jv = Sum of no. of joints per unit length of all discontinuity sets
known as the volumetric joints count.
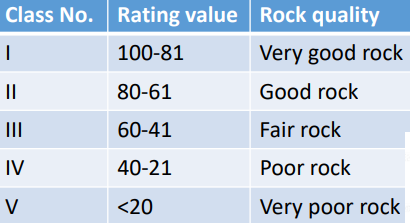
Rock are classified into various groups based on RQD:

c) Rock mass rating system (RMR)/ Bieniawski’s/ Geomechanical classification System

Bieniawski (1976) published the details of a rock mass classification
called the Geomechanics Classification or the Rock Mass Rating (RMR)
system. He has given different rating to different parameter. The sum of
the rating of individual parameter gives the final rating value. The RQD is
used to classify a rock mass using RMR system are:
a) Uniaxial compressive strength of rock material
b) Rock quality designation RQD
c) Spacing of discontinuities
d) Condition of discontinuities
e) Ground water conditions
f) Orientation of discontinuities

Each of the six parameters is assigned a value corresponding to the characteristic of the rock. These values are desired from field surveys and laboratory tests as given in table below:

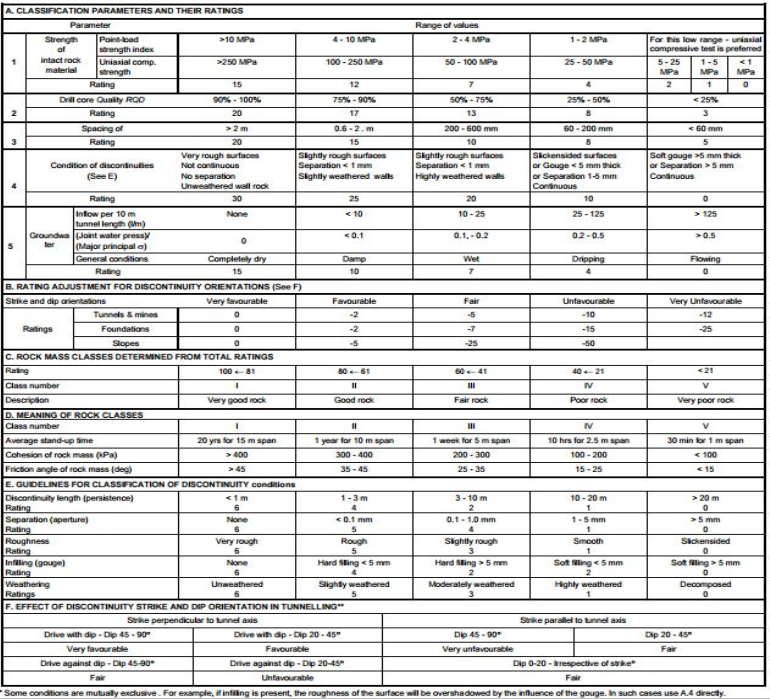
Classification based on RMR

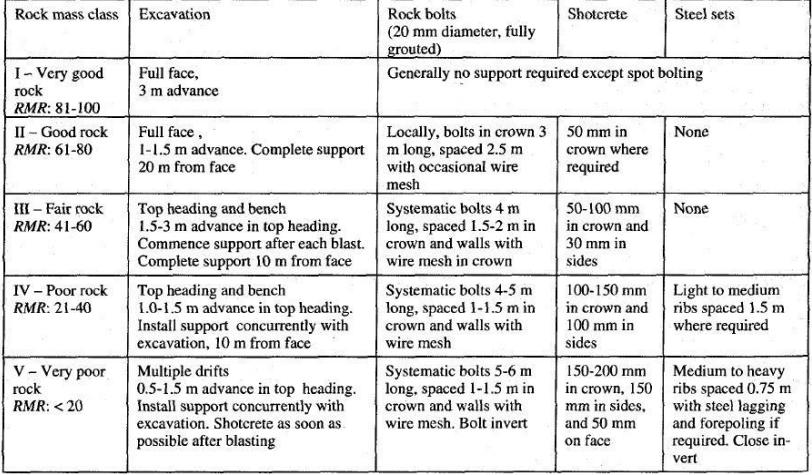
Guidelines for excavation and support of 10 m span rock tunnels in accordance with the RMR system (After Bieniawski 1989).

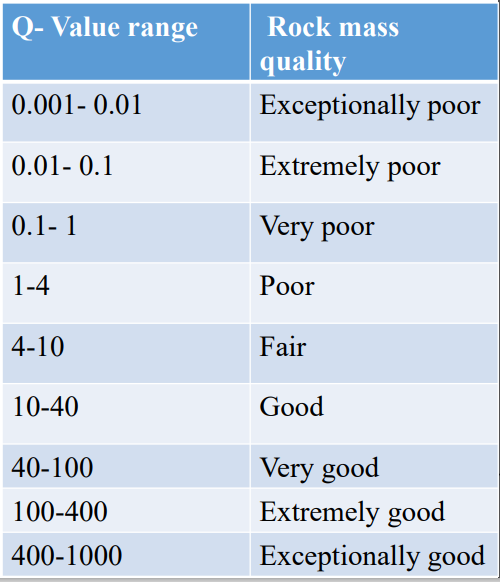
d) Rock Tunneling Quality Index (Q- Value)

On the basis of an evaluation of a large number of case histories of underground
excavations, Barton et al (1974) of the Norwegian Geotechnical Institute proposed a
Tunnelling Quality Index (Q) for the determination of rock mass characteristics and
tunnel support requirements. The numerical value of the index Q varies on a
logarithmic scale from 0.001 to a maximum of 1,000 and is defined by:

Based on Q-value, rock mass is classified in various group as follows:

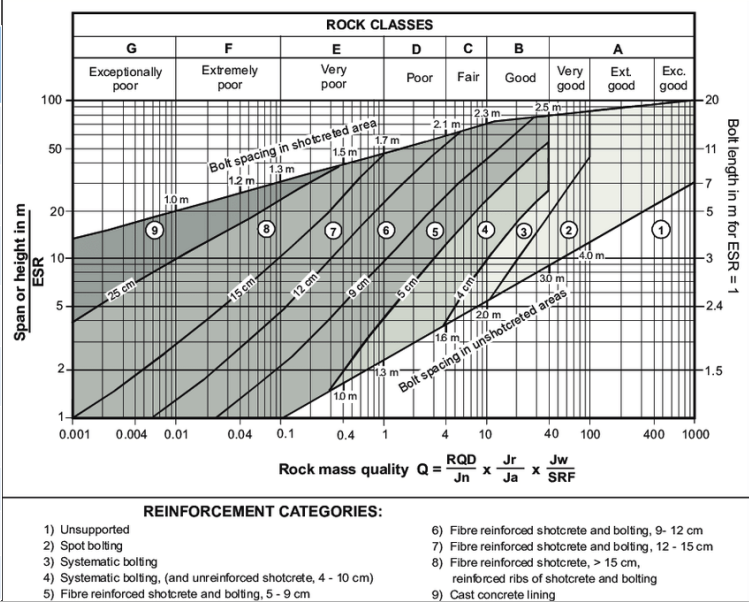
Permanent support recommendations based on Q-values and span/ESR

Slope Stability Analysis:

• Slope stability refers to the condition of inclined soil or rock slopes to withstand or undergo movement. The stability condition of slopes is a subject of study and research in soil mechanics, geotechnical engineering and engineering geology.
• Slope stability analyses include static and dynamic, analytical or empirical methods to evaluate the stability of earth and rock-fill dams, embankments, excavated slopes, and natural slopes in soil and rock. The analyses are generally aimed at understanding the causes of an occurred slope failure, or the factors that can potentially trigger a slope movement, resulting in a landslide, as well as at preventing the initiation of such movement, slowing it down or arresting it through mitigation countermeasures.