Solution of Non- Linear Equation

Bisection Method:

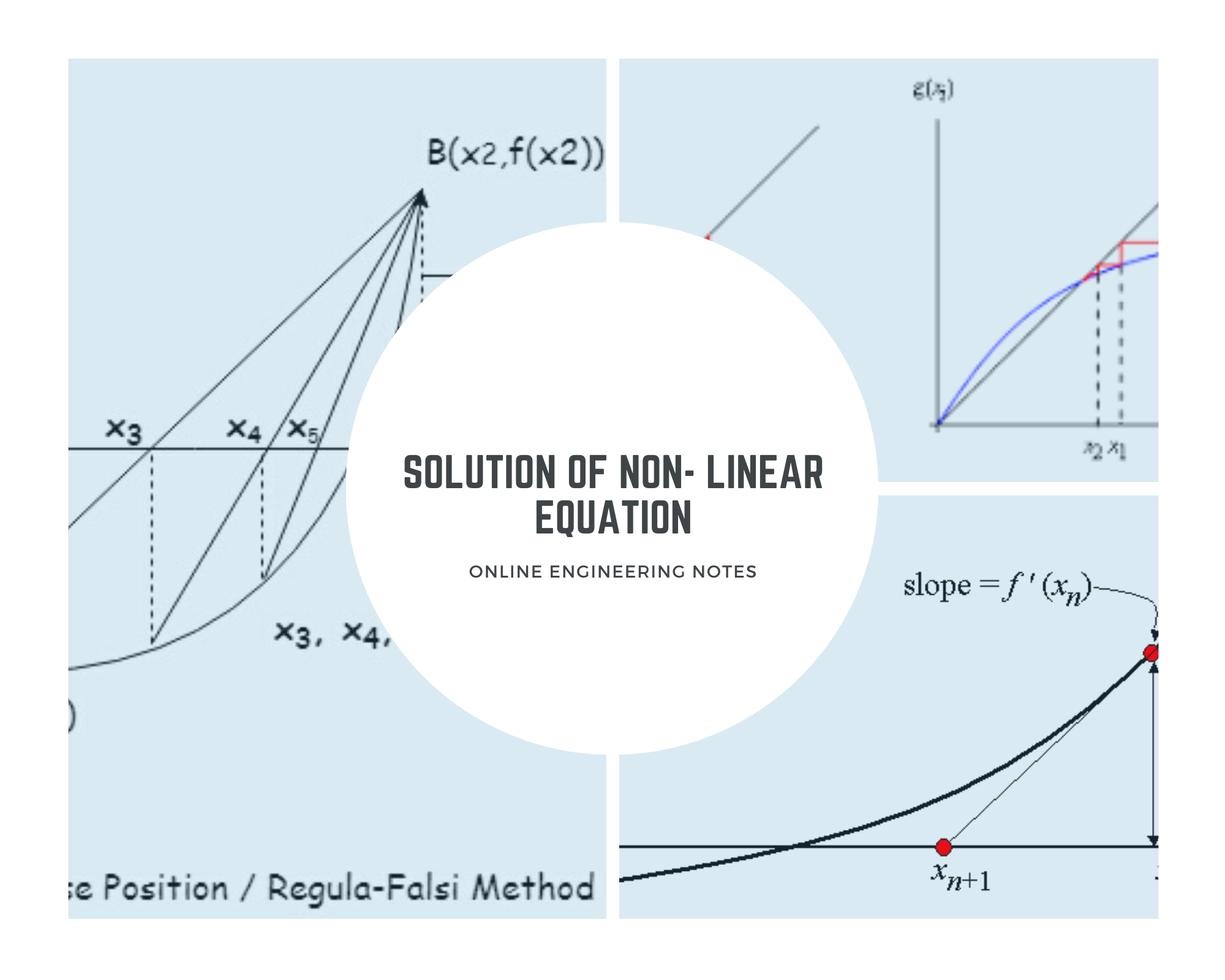
This method is based on the repeated application of intermediate value property. Let, F(x) be continuous between a and b.

Consider,

F(a) be negative and F(b) be positive.

Then, the first approximation of the root is x₁= (a+b)/2 , if F(x₁)= 0 then x₁ is root of F(x)=0.

Otherwise, the root lies between a and x₁ or x₁ and b, according as F(x₁) is positive or negative.

Then, we bisect the interval as before and continue the process until the root is found accuracy.

Problem: (By Bisection Method)

QNo.1 Find the real roots of the equation x³-2x-5=0

Solution:

Given,

Let,

F(x) = x³-2x-5

F(0) = -5

F(1) = -6

F(2) = -1

F(3) = 16

Also,

x₁ = (a+b)/2

or, x₁ = (2+3)/2 = 2.5

F(2.5) = (2.5)³ – 2*2.5-5 = 5.6250

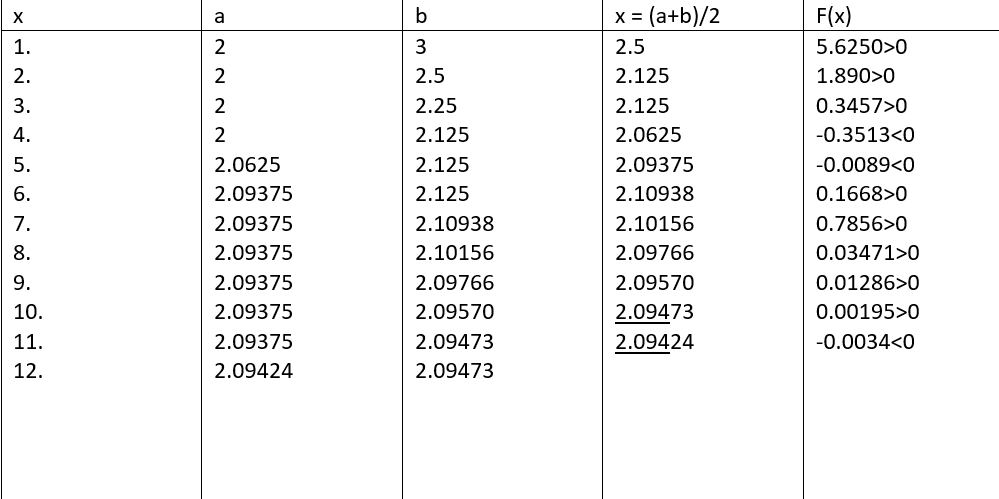
Hence, the real root of the equation is 2.094.

False Position Method (Regula-Falsi Method)

Slope of AB = Slope of AC

Or, {F(b)-F(a) }/(b-a) = {0-F(a)}/(c-a)

Or, c-a = {-F(a) * (b-a)} / { F(b) – F(a)}

Or, c = a – {F(a) * (b-a)} / { F(b) – F(a)}

∴ c =  {a *F(a) – bF(a) } / {F(b) – F(a)}

Working Procedure (Method):-

1. Find the interval (a,b)

 Straight F(a) F(b) <0

2. Find c = {a* F(a) – bF(a) } / {F(b) – F(a)}

3. F(a) F(c) <0 roots lies in (a,c) & F(b) F(c)<0 roots lies in (c,b)

4. Repeat step (1.) and (2.)

Problem: ( By False Position Method)

Qno.1 Find a real root of x³-2x-5=0 using the method false position upto four iteration.

Solution:

Let, F(x) = x³-2x-5

        F(2) = -1

        F(3) = 16

Now,

I- interation

a=2, F(a)= -1

b=3,F(b)= 16

Using the formula, we get

 c = {a* F(a) – bF(a) } / {F(b) – F(a)}

or, c= (32+3)/(16+1) = 2.0588

F(c)= F(2.0588)= -0.3908<0

II-interation

a= 2.0588, F(a) = -0.3908

b= 3, F(b) = 16

c = {a* F(a) – bF(a) } / {F(b) – F(a)}

or, c= {16(2.0588)+3(0.3908)}/(16+0.3908) = 2.0812

F(c) = F(2.0812) = -0.1479

III-interation

a=2.0812, F(a) = -0.1479

b= 3 , F(b) = 16

c = {a* F(a) – bF(a) } / {F(b) – F(a)}

or, c = {16(2.08120)+3(0.1479)}/(16+0.1479)= 2.0896

F(c)=F(2.0896)=-0.0551<0

IV-interation

a=2.0896, F(a) = -0.0551

b= 3 , F(b) = 16

c = {a* F(a) – bF(a) } / {F(b) – F(a)}

or, c = {16(2.0896)+3(0.0551)}/(16+0.0551)= 2.0927

Hence, the required root is = 2.0927.

Fixed Point Iteration Method (Iteration Method)

Suppose we have equation F(x) = 0. The equation can be expressed as x = ϕ(x)

At x= x₀

|ϕ^| (x) |< 1

Then, iterative method applied. The suceesive approximation is

Given by x_n= ϕ(x_n-1)

                x₁= ϕ(x₀)

                x₂= ϕ(x₁)

Now,

x_n = 1 / (1+ x_n-1)^1/2

Problem: (By Fixed Point Iteration Method)

Qno1. Find the roots of cosx = 3x -1, correct to four decimal places by iteration method.

Solution:

Let,

F(x) = cosx – 3x+1

F(0)= 2

F( π/2) = 0 – (3 π/2)+ 1 < 0

Now,

x =  ϕ(x) —————————-(i)

So, taking equation

Cosx = 3x-1

Or, 3x = 1 + cosx

Or, x = (1+ cosx)/3

Now,

Equation (i) is

ϕ(x) = (1+ cosx)/3

Differentiating on both side w.r.t x

|ϕ^| (x) | = |sinx/3 |

At x₀ = 0

|ϕ^| (x) | = |sin0/3 | <1

Or, |ϕ^| (x) | = 0 <1

Now,we  can apply equation

x= (1+cosx)/3

Now,

x_n = (1+ cos x_n-1)/3

Put, n=1

x₁ = (1+cos x₀)/3 = 0.066667

Put, n = 2

x₂ = (1+ cos (0.066667) * 57.3)/3 = 0.595296

x₃ = (1+cos(0.595296)* 57.3)/3 = 0.609328

x₄ = (1+cos(0.609328)* 57.3)/3 = 0.606678

x₅ = (1+cos(0.606678)* 57.3)/3 = 0.60782

x₆ = (1+cos(0.60782)* 57.3)/3 = 0.607086

x₇ = (1+cos(0.607086)* 57.3)/3 = 0.607105

x₈ = (1+cos(0.607105)* 57.3)/3 = 0.607101

The correct root to four decimal places is 0.6071.

Secant Method ( Chord Method)

This method is quite similar to false position method except for the condition F(x₁) F(x₂) < 0.

Slope of AB = Slope of AC

Or, x-x₀ = – {F(x₀)(x₁-x₀)}/{ F(x₁) – F(x₀)}

Or, x = {x₀F(x₁) – x₁F(x₀)}/ { F(x₁) – F(x₀)}

Now,

x_n+2 = {x_nF(x_n+1) – x_n+1F(x_n)}/{F(x_n+1) – F(x_n)}

This method fails when F(x_n) = F(x_n+1).

Problem:( By Secant Method)

Qno.1. Estimate the root of the equation cosx-xe^x= 0 . Using the secant method with initial estimate of x₁ = 0.5 , x₂=1.

Solution:

F(x) = cosx – xe^x

F(x₁)=F(0.5)= cos(0.5) – (0.5) e^(0.5) = 0.0532

F(x₂)=F(1)= cos(1) – (1) e⁽¹⁾ = -2.17798

x_n+1 = {x_n=1 F(x_n) – x_nF(x_n-1)}/ {F(x_n)- F(x_n-1)}

Put, n=2

x₃ = {x₁F(x₂)-x₂F(x₁)} / {F(x₂) – F(x₁)} = 0.5119

F(x₃) = F(0.5119)= cos(0.5119) – (0.5119) e^(0.5119) = 0.01773

Put, n=3

x₄ = { x₂F(x₃)-x₃F(x₂)} / {F(x₃) – F(x₂)} = 0.5158

F(x₄) = F(0.5158)= cos(0.5158) – (0.5158) e^(0.5158) = 0.00544

Put, n=4

x₅ = { x₃F(x₄)-x₄F(x₃)} / {F(x₄) – F(x₃)} = 0.5178

F(x₅) = F(0.5178)= cos(0.5178) – (0.5178) e^(0.5178) = 0.00012

Put, n=5

x₆ = { x₄F(x₅)-x₅F(x₄)} / {F(x₅) – F(x₄)} = 0.5178

F(x₅) = F(0.5178)= cos(0.5178) – (0.5178) e^(0.5178) = 0.00012

Hence, the root of the equation is 0.5178.

Newton Raphson Method

Equation of Tangent

y-F(x₀) = F^’(x₀) (x₁-x₀)

or, 0-F(x₀) = F^’(x₀) (x₁-x₀)

or, x₁-x₀= -F(x₀) / F^’(x₀)

or, x₁ = x₀ -F(x₀) / F^’(x₀)

Now,

x_n+1 = x_n -F(x_n) / F^’(x_n) ,  F^’(x_n)  ≠ 0

Problem: ( By Newton Raphson Method)

Qno1. Find by Newton Raphson Method a root of equation x³-3x- 5 = 0.

Solution:

F(x)= x³-3x- 5

F(2)= -3

F(3)= 16

Now,

F^’(x) = 3 x²– 3

Using Formula,

x_n+1 = x_n -F(x_n) / F^’(x_n)

or, x_n+1 = x_n – (x_n³-3 x_n – 5)/(3 x_n ²– 3)

Put, n=0

x₁ = x₀ – (x₀³-3 x₀ – 5)/(3 x₀ ²– 3) = 2.3333

Put, n=1

x₂ = x₁ – (x₁³-3 x₁ – 5)/(3 x₁ ²– 3) = 2.2805

Put, n=2

x₃ = x₂ – (x₂³-3 x₂ – 5)/(3 x₂ ²– 3) = 2.2790

Put, n=3

x₄ = x₃ – (x₃³-3 x₃ – 5)/(3 x₃ ²– 3) = 2.2790

Hence, the required root is 2.2790.