1.1 Phase Diagram, basic definition & functional relationship
Soil mass consists of solid soil particles containing void space between them. Space between the soil particles is known as void and these void is filled with either air or water or both.
The diagrammatic representation of the different phases in a soil mass is called phase diagram.
When soil masses consist of air, water and solid particles it is known as three phase system.
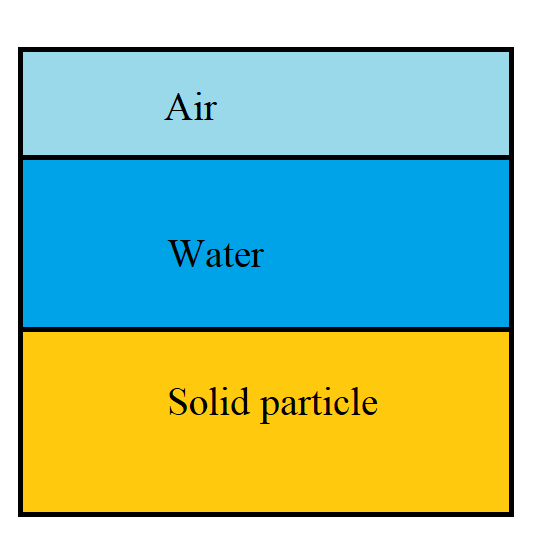
When soil masses consist of water and solid particle it is known as two phase system for saturated soil.
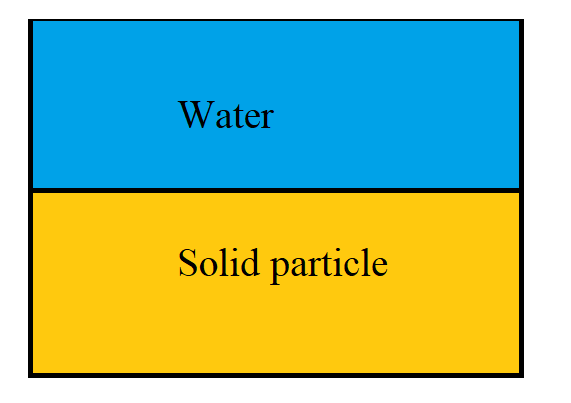
When soil masses consist of air and solid particle it is known as two phase system for dry soil.

Equation of three phase system:
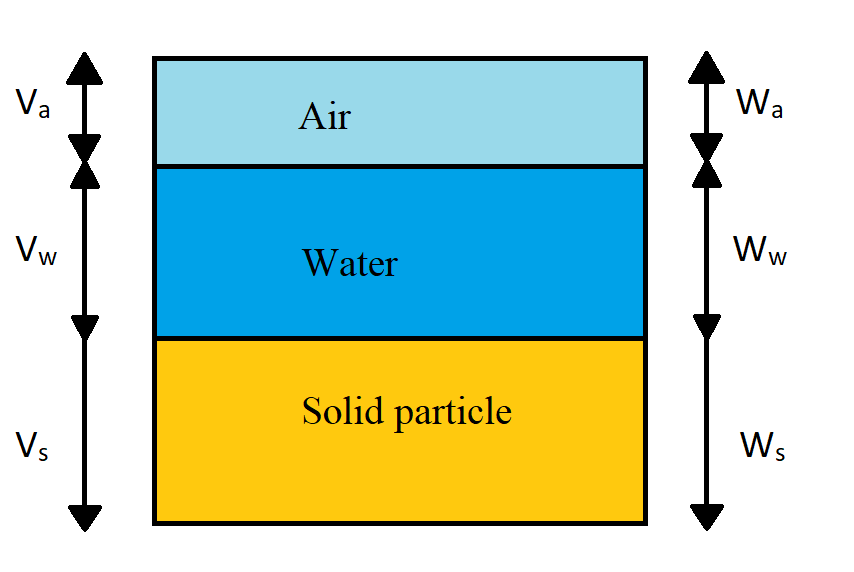
Let,
V = Total volume of soil
Vs = Volume of solid particle
Va = Volume of air
Vw = Volume of water
Vv = Volume of void
So, from the definition of
Total volume of soil is equal to the sum of volume of air, water and solid particle respectively.
i.e. V = Vw + Va + Vs
or, V = Vs + Vv [∴Vw + Va ]
Similarly,
For weight
Total weight (W) = Weight of solid (Ws) + Weight of water (Ww) + Weight of air (Wa)
i.e W = Ws + Wa + Ww
Also,
Weight of void (Wv) = Wa + Ww
or, Wv = Ww [∴ Weight of air is negligible, so Wa =0 ]
∴ Wv = Ww
Total weight of soil mass,
W = Ws + Ww
Similarly, in terms of mass
M = Ms + Mw
Some important terms:
1. Void ratio (e) = Volume of void (Vv) / Volume of solid (Vs)
2. Porosity (n) = Volume of void (Vv) / Total volume (V)
3. Degree of saturation (S or Sr)
or, S = Volume of water (Vw) / Volume of void (Vv)
4. Air content (ac) = Volume of air (Va) / Volume of void (Vv)
5. Percentage of air void (na) = Volume of air (Va) / Total volume (V)
6. Water content or Moisture content (w) = Weight of water (Ww) / Weight of solid (Ws)
7. Unit weight (γ) = Weight (W) / Volume (V)
a. Bulk unit weight (γ) = W / V
or, γ = (Ws + Wv) / ( Vs + Vv)
b. Dry unit weight (γd) = Ws / V
c. Saturated unit weight (γsat) = Wsat / V
d. Submerged unit weight (γsub) = Wsub / V
or, γsub = γsat – γw
or, γI = γsat – γw
e. Unit weight of solid (γs) = Ws / Vs
8. Specific gravity (G) = (Ms / Mw)
or, G = (Ms / Mw) = (ρs / ρw) = (γs / γw)
At 4o C
ρw = 1000 kg/m3 = 1g/ml
γw = 9810 N/m3 = 9.81 KN/m3
Some important relation:
a. Relationship between e,w,Sr and G
We know,
e = Vv / Vs
or, e = (Vv / Vw) * (Vw / Vs)
or, e = (Vv / Vw) * (Ww / γw) * (γs / Ws)
or, e = (Vv / Vw) * (Ww / Ws) * (γs / γw)
or, e = (Vv / Vw) * w * G [∴ w = (Ww / Ws), G = (γs / γw) ]
or, e = (1/Vw / Vv ) * G * w
or, e = (1 / Sr) * w * G
or, Sr * e = w * G
∴ Sr * e = w * G
b. Relationship between e and n
n = Vv / V = Vv / (Vv + Vs)
or, 1/n = (Vv + Vs) / Vv
or, 1/n = 1 + (Vs / Vv)
or, 1/n = 1 + 1/Vv /Vs [∴ e = Vv / Vs]
or, 1/n = 1 + 1/e
or, 1/n = (e+1)/e
or, n = e / (e+1)
or, n(e+1) = e
or, e = ne + n
or, e = n / (1-n)
∴ e = n / (1-n)
c. Relationship between unit weight (γ) in terms of terms of water content (w), void ratio (e), specific gravity (G) and γw.
We know,
γ = W / V = ( Ws + Wv) / ( Va + Vs + Vw)
or, γ = ( Ws + Ww) / ( Vv + Vs) [∴ Ww = Wv]
or, γ = (Ws / Vs) * {(1 + Ww / Ws) / (1 + Vv / Vs)}
or, γ = γs * (1 + w) / (1+ e) ————–(1)
[∴w = (Ww / Ws), e = Vv / Vs ]
Also,
G = γs / γw
or, γs = G γw
Now, From equation (1) become,
∴γ= G γw (1 + w) / (1+ e)
d. Relationship between γ, G, Sr, e and γw.
We know,
γ = W / V
or, γ = (Ws + Wv) / (Vs + Vv)
or, γ = (Ws / Vs) * { (1 + Wv / Ws) / ( 1 + Vv / Vs) }
or, γ = γs * (1 + w) / (1 + e)
or, γ = G γw * (1 + w) / (1 + e)
or, γ = γw * { (G + Gw) / (1+e) } ————–(1)
We know,
Sre = wG ————-(2)
From equation (1) and (2), we get
∴ γ = γw * { (G + Sre) / (1+e) }
Condition:
- If soil is fully saturated Sr = 1 (100%)
γ as γsat
∴ γsat = γw * { (G + e) / (1+e) }
- If soil is dry then Sr = 0 (0%)
γ as γd
∴ γd = (γw * G)/ (1+e)
e. Relation between dry unit weight (γd), Bulk unit weight (γ) and water content (w).
We have,
w = Ww / Ws
Adding one on both side
w + 1 = (Ww + Ws) / Ws
or, w + 1 = (Ww + Ws) / Ws
or, w + 1 = W / Ws
or, Ws = W / (w + 1) ———–(1)
Also,
γd = Ws / V ————(2)
From equation (1) and (2)
γd = W / (w + 1) * 1 / V
or, γd = W / V (1 + w)
or, γd = W / V * 1 / (1+w)
or, γd = γ* 1 / ( 1 + w) [∴γ = W / V]
∴ γd = γ/ (1 + w)
f. Relationship between submerged unit weight (γI), specific gravity of solid (G) and void ratio (e).
We have,
γsub or γI = γsat – γw
But,
γsat = {(G + e) γw} / (1+e)
Now,
γI = {(G + e) γw / (1+e)} – γw
or, γI = {(G+e) γw – γw(1+e)} / (1+e)
or, γI = γw(G-1) / (1+e)
∴ γI = γw(G-1) / (1+e)
g. Relationship between dry unit weight (γd), specific gravity of solid (G), water content (w) and percentage of air void (na).
We have,
V = Vs + Va + Vw
or,V = Va + (Ww / γw) + (Ws / γs)
[∴γ = Ww / Vw, Simillarly γs = Ws / Vs]
Dividing both side by V, we get
1 = (Va / V) + (Ww / Vγw) + (Ws / Vγs)
But,
w = Ww / Ws
or,Ww = w * Ws
Now,
1 = na + {(w * Ws) / ( V * γw) } + Ws / V * γs
[∴ na = Va / V]
or, 1 – na = (Ws / V) * {(w / γw) + (1 / γs)}
or, 1 – na = (Ws / γw * V) * (w + γw / γs)
or, 1 – na = (Ws / γw * V) * (w + 1 / G)
[∴ G = γw / γs]
or, 1 – na = (γd / γs) *(w + 1 / G)
[∴γd = Ws / V]
or, γd = {(1-na) G γw} / (1 + wG)
When na = 0 (Fully saturated)
∴ γd = G γw / (1 + wG)
1.2 Index properties and their determination for coarse and fine grained soil
The properties of soil which helps to know engineering behaviors of soil and also helps to determine the classification of soil accurately is called index properties of soil.
The list of index properties:
- Water content
- Specific gravity of soil
- Field ( In – situ) density
- Particle size distribution
- Consistency limit and indices
- Density index
1.2.1 Determination of Various Index Properties:
1. Determination of water content
a. Oven drying method:
Process:
- Take a clean container and weight the container.
- Take about 100 gm wet sample and weight it again.
- Keep the soil with container in oven for overnight by maintain 104o C temperature.
- After drying find the weight of dry soil and container.
Calculation:
Weight of container = W1
Weight of container + Wet soil = W2
Weight of container + Dry soil = W3
Water content (w) = (Ww / Ws) * 100%
or, w = {(W2 – W1) / (W3 – W1)} * 100%
2. Determination of specific gravity
a. Pycnometer method:
Process:
- Take empty pycnometer.
- Take about 200 gm of dry sample in pycanometer and weight it.
- Add water in pycnometer and weight it.
- Take empty pycnometer and fill with water and weight it.
Calculation:
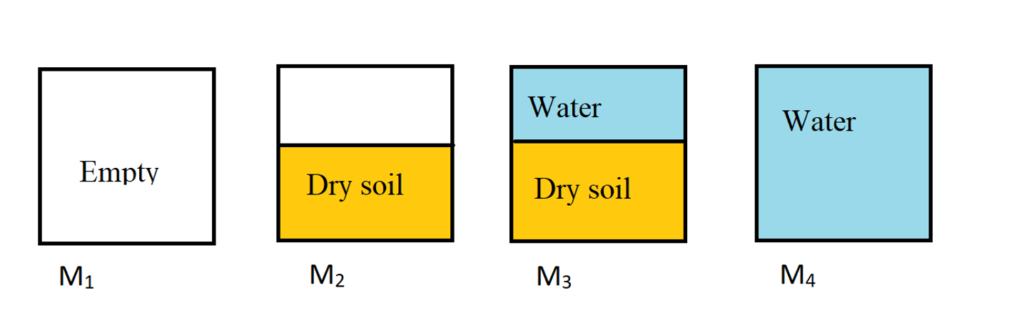
M1 = Mass of empty pycnometer
M2 = Mass of dry sample fill in pycnometer
M3 = Mass of wet sample ( saturated sample)
M4 = Mass of water in pycnometer
Ms= Mass of dry soil
Now,
M4 = M3 – Ms + Mw
or, M4 = M3 – Ms + Vs *ρw
or, M4 = M3 – Ms + Ms * (1 / G) ————(1)
[∴ G = ρs / ρw]
Also,
Ms = M2 – M1
Putting the value in equation (1).
M4 = M3 – M2+ M1 + (M2 – M1) / G
or, M4 – M3 + M2 – M1 = (M2 – M1) / G
or, G = {( M2 – M1) / (M4 – M3 + M2 – M1)}
or, G = ( M2 – M1) / (M4 + M2) – (M1 + M3)
∴ G = ( M2 – M1) / (M4 + M2) – (M1 + M3)
3. Determination of field density
a. Core cutter method
Process:
- Take a clean core cutter.
- Clean and level the ground where density is to be measured.
- Press cylinder cutter into the ground to its full depth with the help of rammer.
- Remove the core cutter from the soil.
- Take the mass of cutter and soil.
Calculation:
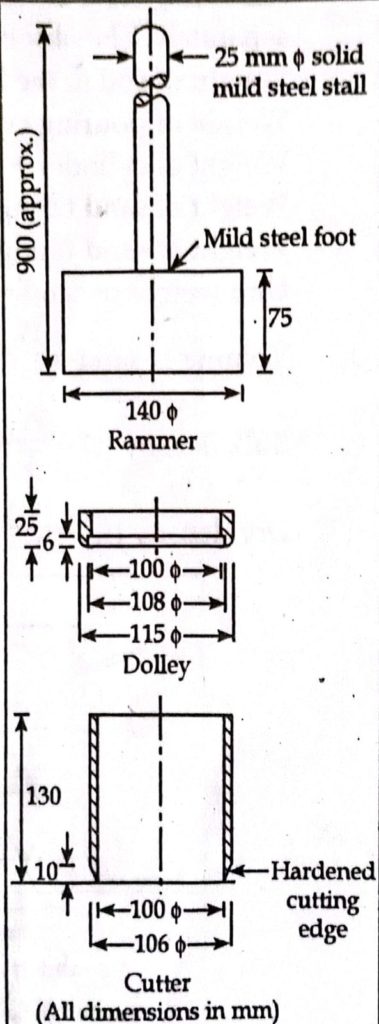
M1 = Mass of clean core cutter
M2 = Mass of cutter with soil
H = Height of cutter
d = Diameter
A = Area of cutter
Now,
Mass of soil (M) = M2 – M1
Volume of soil = A * H = (πd2/4)* H
Where,
H = 130 mm
d = 100 mm
Then,
Density (ρ ) = M/V
b. Sand replacement method:
Process:
- The site is cleaned and a square tray with a central hole is place on the surface.
- The hole of diameter is equal to the diameter of hole in tray.
- The excavated soil is collected in tray and weighted and water content is determined.
- The pouring cylinder is fitted with sand to about ¾ capacity and weight is taken and also its density is found out.
- The cylinder is then place over the hole and tap is opened and sand is allowed to run to fill the excavated whole and conical end.
- When no further flow of sand takes place, the tap is closed and bottle with remaining sand is weighted. The weight of sand filling the cone of bottle is taken separately.
Calculation:

Weight of soil in the hole = W1
Weight of pouring cylinder + sand before pouring = W2
Weight of cylinder + sand after pouring = W3
Weight of sand filling conical funnel = W4
Weight of sand filling hole = W2 – W3 – W4
Unit weight of sand = γ
Now,
Volume of sand = (W2 – W3 – W4) / γ
= Volume of hole = V
Bulk density (γ) = W1 / (1 + w)
Dry density (γd) = γ / (1+w)
4. Particle Size Distribution:
a. Sieve analysis:
- Sieve is utensil made up of spun brass having size of square opening in mm or microns (80mm – 75µ) and diameter of sieve is 15-20 cm and used for separating coarse and fine grained soil.
- Sieve analysis is done for coarse grained soil.
- Gravel: Size greater than 4.75mm.
- Sand: Size in between 75 µ to 4.75mm.
- The sieves are stacked one over the other with decreasing size from top to bottom. The sieve of largest opening is kept at the top to bottom. The sieve of largest opening is kept at the top. A lid or cover is place at the top of largest sieve. A receiver known as pan which has no opening is placed at the bottom of smallest sieve.
- There are two type of sieve analysis:
- Dry sieve analysis
- Wet sieve analysis
b. Sedimentation analysis:
Sedimentation analysis or wet mechanical analysis is conducted on soul fraction finer than 75micron which is kept in suspension in a liquid medium usually water.
Sedimentation analysis is based in Stoke’s Law according to which gives the terminal velocity of small sphere setting in a fluid of infinite extent.
Now,
Terminal velocity (v) = {gD2 * (G – 1) ρw} / 18η ———(1)
If a particle fall through height He in “t” minutes,
v = He / 60t ————-(2)
Combining equation (1) and (2)
D = M (He / t)1/2
Where,
M = {30η / g(G – 1) ρw }
Uses of Particle size distribution curve:
- Classification of coarse grained soils.
- Determination of coefficient of permeability.
- To know susceptibility of soil to frost action.
- Design of drainage filter.
- Determination of shear strength of soil.
- Compressibility of soil.
- Used for soil stabilization.
- Design of pavement.
- Indicate mode of deposition of soil.
- Age of soil deposit.
5. Consistency of soil:
- The physical state of fine grained soil at particular water content is known as consistency.
- Mostly used for fine grained.
- The limiting water content at which a soil passes from one state of consistency to another state is called consistency limit.
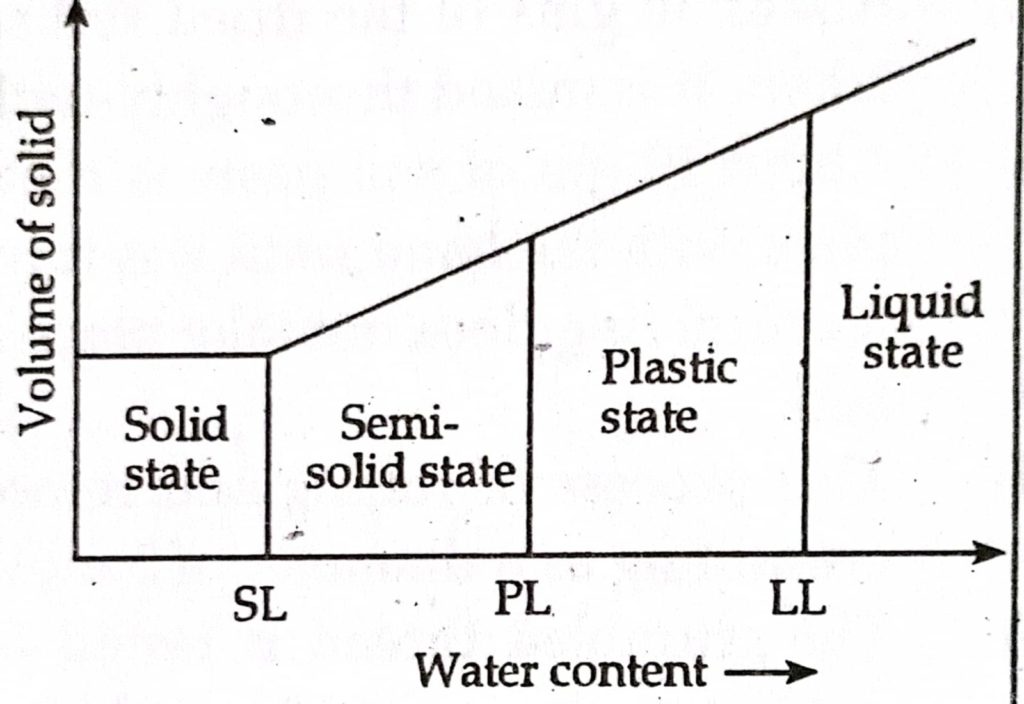
Determination of consistency limit:
a. Liquid limit (LL):
At liquid limit, the soil possesses a small value of shear strength. The liquid limit is the minimum water content at which the soil is still in liquid state but has a small shearing strengh agaist flowing.
b. Plastic Limit (PL):
In plastic limit soil can be moulded into any shape.
wp = Ww / Ws = (W1 – W2) / W2
where,
W1 = Weight of soil before drying
W2 = Weight of soil after drying
c. Shrinkage limit:
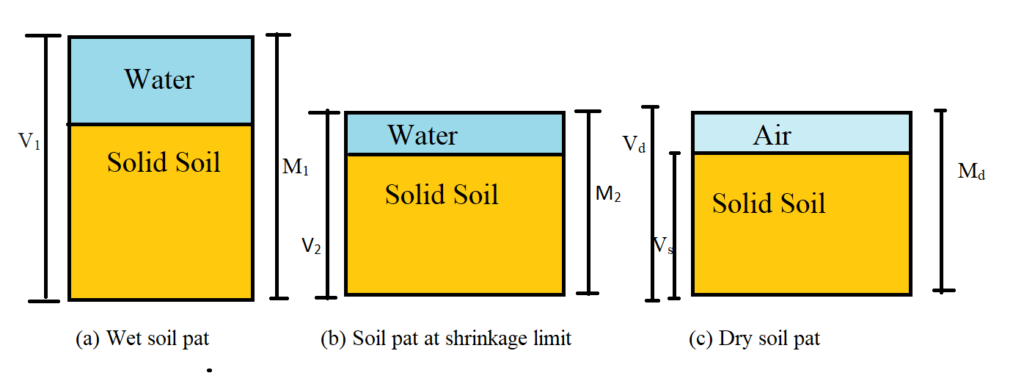
In shrinkage limit water content is lowest.
ws = {(M1 – Md) – (V1 – γd) γw} / Md
Where,
M1 = Mass of wet soil pat
V1 = Volume of wet soil pat
Md = Mass of fry soil pat
Vd = Volume of dry soil pat
Or,
ws = {(Vd γw) / Md} – 1/G
References:
- Terzaghi, Karl, Peck, R.B & John, Wiley (1969) Soil mechanics in engineering practice, New York.
- Arora , K.R (2008), Soil mechanics and foundation engineering, Delhi: Standard Publisher Distribution.

