Introduction to open channel flow and its practical application:
- Open channel flow is defined as the flow of a liquid with a free surface i.e. surface having constant pressure such as atmospheric pressure.
- Rivers, streams, canals and irrigation ditches are the example of open channel flow.
Difference between open channel and pipe flows:
- Open channel flow has a free water surface.
- Open channel flow is subjected to atmospheric pressure while pipe is not subjected to atmospheric pressure.
- Open channel flow is not completely enclosed by boundaries , unlike pipe flow.
- Open channel is always under the action of gravity , while pipe can be under gravity or may flow due to some external pressure.
Classification of Open Channel:
On the basis of shape :
- Rectangular channel:
A channel which is rectangular in shape is called rectangular channel.
- Triangular channel:
A channel which is triangular shape is called triangular channel.
- Trapezoidal channel:
A channel which is trapezoidal in shape is called trapezoidal channel.
- Circular channel:
A channel which is circular in shape is called circular channel.
On the basis of occurrence:
- Natural channel:
Nature channel are generally irregular in shape, alignment and roughness of the surface.
Example: Streams, rivers, valley etc.
- Artificial channel :
Artificial channel are built for some specific purpose, such as irrigation, water supply, waste water, water power development and rain collection channels. These are regular in shape and alignment with uniform roughness of the boundary surface.
On the basis of boundary:
- Prismatic channel:
In this type of channel slope and cross section both don’t change.
- Non-Prismatic channel:
In this type of channel both slope and cross section or only slope or cross section change.
- Rigid channel:
In this type of channel boundary of channel do not change.
Example: Lined channel.
- Mobile channel:
In this type of channel boundary of channel will change.
Example: River, unlined channel.
Types of open channel flow:
On the basis of time:
- Steady flow:
A flow in which the velocity, depth of flow and discharge of the fluid at a particular fixed point does not change with time.
Mathematically,
∂v/∂t = 0 ,
∂Q / ∂t = 0 and
∂y / ∂t = 0
Where,
v= Velocity
Q= Discharge
y =Depth of flow
- Unsteady flow:
A flow in which the velocity , discharge (i.e. rate of flow) and depth of flow of the fluid change with time.
Mathematically,
∂v/∂t ≠ 0,
∂Q / ∂t ≠ 0 and
∂y / ∂t ≠ 0
Where,
v= Velocity
Q= Discharge
y =Depth of flow
On the basis of space\length:
- Uniform flow:
If for a given length of the channel, the velocity of flow, depth of flow, slope of the channel and cross- section remain constant, the flow is called uniform flow.
Mathematically,
∂v/∂s = 0 ,
∂y / ∂s = 0
2. Non-Uniform flow:
If for a given length of the channel, the velocity of flow, depth of flow, slope of the channel and cross-section donot remain constant the flow is called non-uniform flow.
Mathematically,
∂v/∂s ≠ 0 ,
∂y / ∂s ≠ 0
Also, non-uniform flow in open channels is also called varied flow.
Types of Non-Uniform flow:
- Rapidly varied flow(R.V.F)
It is defined as the flow in which depth of flow changes abruptly over a small length of the channel.
- Gradually varied flow(G.V.F)
It is defined as the flow in which depth of flow in a channel changes gradually over a long lengh of the channel,
- Spatially varied flow(S.V.F)
It is defined as the flow in which depth of flow changes gradually due to change in discharge.
On the basis of regime:
On the basis of Reynolds number:
- Laminar flow:
It is defined as the type of flow in which the fluid particles move along well-defined paths or stream lines and all the stream lines and all the stream lines are straight and parallel.
Reynolds number(Re) is less than 500 or 600.
- Turbulent flow:
It is defined as the type of flow in which the fluid undergoes irregular fluctuations, or mixing, in contrast to laminar flow, in which the fluid moves in smooth paths or layers.
Reynolds number (Re) is more than 2000.
- Transitional flow:
The flow occurs between laminar and turbulent flow. Reynolds number ( Re) lies between 500 to 2000.
Mathematically,
Re= (ρvR)/ μ
On the basis of Froude number(Fr)
- Critical flow:
The flow in open channel is said to be critical flow if the Froude number(Fr) is equal to 1.
- Subcritical flow:
The flow in open channel is said to be critical flow if the Froude number(Fr) is less than 1.
- Supercritical flow:
The flow in open channel is said to be supercritical flow if the Froude number(Fr) is greater than 1.
Geometric properties of open channels:
Trapezoid:
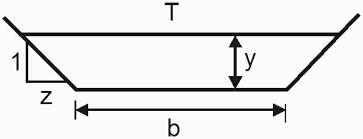
- Depth of flow = y
- Depth of flow section(y’)
y’ = ycosθ
- Top width(T)
T= B+2zy
- Area(A)
A = ( B+zy)y
- Wetted perimeter(P)
P= B+2y (Z2 + 1)1/2
- Hydraulic radius(R)
R= A/P

2. Rectangle

- Depth of flow= y
- Top width (T)
T= B
- Area(A)
A=By
- Wetted perimeter(P)
P= B+2y
- Hydraullic radius(R)
R= A/P
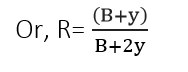
- Hydraullic depth(D)
D=A/T
Or D=y
3.Triangle:

- Depth of flow=y
- Top width(T)
T= 2zy
- Area(A)
A=zy2
- Wetted perimeter(P)
P=2y(z2+1)1/2
- Hydraullic radius(R)
R=A/P
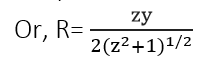
- Hydraulic depth (D)
D= A/T
Or, D= (½ )y
4. Circle
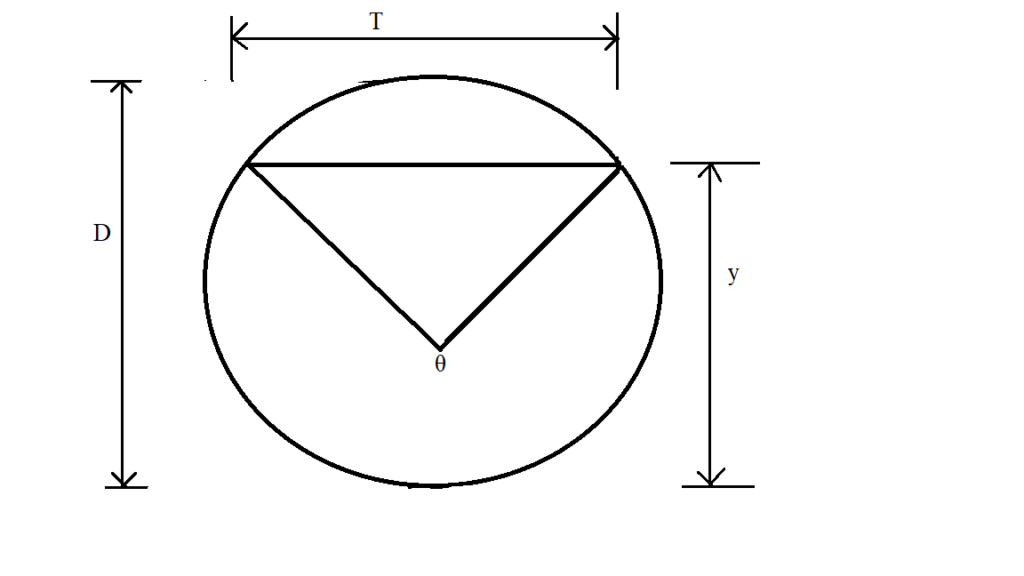
- Depth of flow=y

References: 1. Hydraulics and fluid mechanics including hydraulics machine, Dr. P.N. Modi, Dr. S.M Seth, Rajsons publication.

