Flow Through Pipes

Introduction to pipe flow:

A pipe is a closed conduit (channel) which is used for carrying fluids under pressure. Pipes are commonly circular in section. The fluid in the pipes are subjected to frictional resistance due to shear stress.

Reynolds experiment and flow based on Reynolds number.

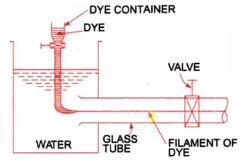
 Reynolds experiment is used to display laminar, transion and turbulent flows. During the experiment it is possible to observe the transion from laminar to turbulent flow after limiting velocity. The Reynolds number is used to assess whether a flow is laminar, transion or turbulent.

The apparatus consists of :

a. A tank containing water at constant head.

b. A small tank containing some dye.

c. A glass tube having a bell-mounted entrance at one end and a regulating value at other ends.

The water from the tank is allowed to flow through the glass tube. The velocity of flow was varied by the regulating valve. A liquid dye having same specific weight as water is introduced into the glass tube as shown in figure.

The following observations were made by Reynolds:

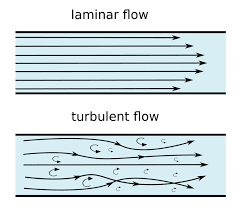
• When the velocity of flow is low, the dye filament in the glass tube was in the form of a straight line. This straight line of dye filament is parallel to the glass tube, which is the case of laminar flow.

• With the increase of flow, the dye filament was no longer a straight-line but it became a wavy one. This shows flow is transion.

• With further increase of velocity of flow, the wavy dye-filament broke-up and finally diffused in water. This shows the turbulent flow.

Now,

R_e = Inertia Force/Viscous Force = F_i / F_v

According to Newton’s second law of motion to inertia force F_i is given by

F_i = mass * acceleration

   = ρ * volume* acceleration

   = ρ*L³*(L/T²)

   = ρL²v²

Similarly,

Viscous force F_v is given by Newtons Law of viscosity as

F_v = Ʈ * area

   = { µ(dv)/(dy)} * L²

   = µvL

Now,

R_e = { ρL²v²} / {µvL}

Where,

ρ =  Density

µ = Dynamic viscosity

v = Velocity of flow

L = Linear dimension

The above equation i.e. dimensionless parameter is called Reynolds number.

Flow based on Reynolds number:

Flow type	Reynolds number range
Laminar	Re<2000
Transion	Re lies between 2000 to 4000
Turbulent	Re > 4000

Laminar flow ( Viscous or Streamline flow)

The flow is consider to be laminar when fluid particles move in a straight path such that the path of individual particle donot cross the path of neighbouring particles ( or they move as gliding smoothly over the adjacent layers.) Laminar flow exist at low velocity.

Example:

a. Underground flow and

b. Blood circulation in the Arteries of human body.

Major Head Loss for Laminar flow through pipe ( Hagen Poisscuille Equation)

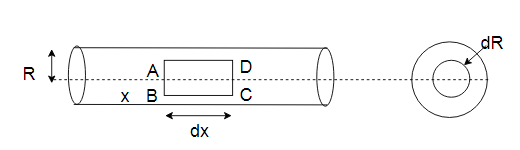
Consider a horizontal pipe of radius R. The viscous fluid is flowing from left to right in the pipe as shown in figure a. Consider a fluid element of radius r, sliding in a cylindrical fluid element of radius ( r+ dr). Let, the lenght of fluid element be △x.

If P is the intensity of pressure on the face AB, then the intensity of pressure on face CD will be (P + ∂P/∂x △x ).

Then,

The forces acting on the fluid element are:

• The pressure force, P*πr² on face AB.
• The pressure force (P + ∂P/∂x △x  ) πr² on face CD.
• The shear force, Ʈ * 2 πr△x on the surface of fluid element.

a. Shear Stress Distribution:

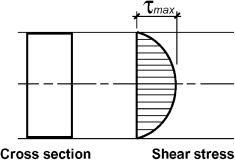
As there is no acceleration, hence the sum of all forces in the direction of flow must be zero i.e.

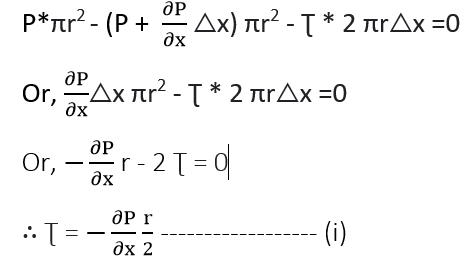
The shear stress Ʈ across a section varies with r as ∂P/∂x across a section is constant. Hence, shear stress distribution across a section is linear.

b. Velocity Distribution:

Taking relation,

Ʈ = µ(du)/(dy)

Here, y is measured from the pipe wall.

Hence,

y = R-r and

dy = -dr

∴ Ʈ = -µ(du)/(dy)

Substituting the value in equation (i)

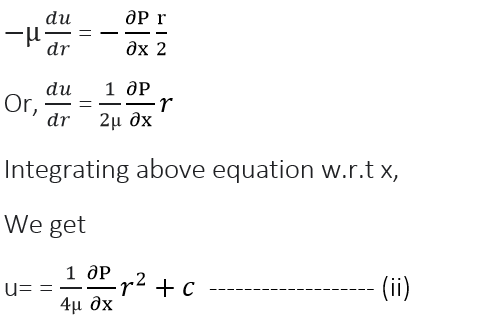
Where,

c= Constant of integration and

 From boundary condition;

r=R, u=0

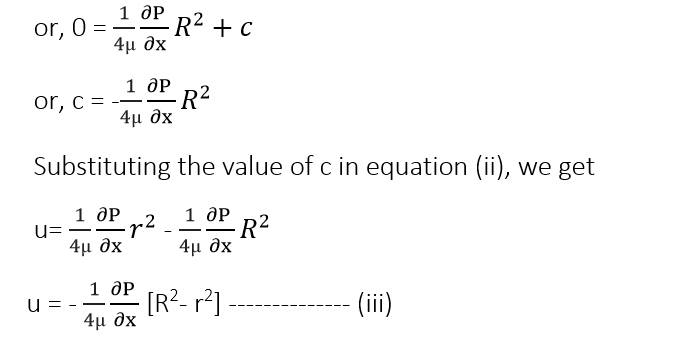
In equation (iii), values of µ, ∂P/∂x and R are constant, which means the velocity, u varies with the square of r. Thus, equation (iii) is a equation of parabola.

c. Ratio of maximum velocity to averange velocity:

The velocity is maximum, when r=0 in equation (iii)

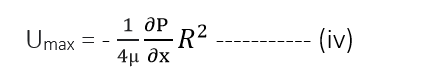
Where, U_max = maximum velocity

Consider the flow through a circular ring element of radius r and thickness dr as shown in figure (b).

The fluid flowing per second through the elementary ring is

dQ = velocity at a radius r * area of ring element

      = u * 2 πrdr  

∴ Ratio of maximum velocity to average velocity = 2.

d. Drop of pressure for a given length (L) of a pipe:

From equation (v) we have,

Integrating the above equation w.r.t  x, we get

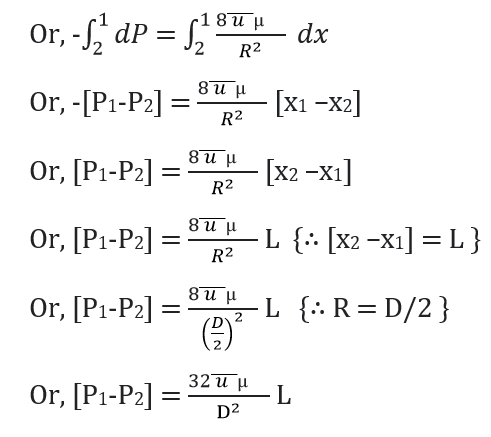
Where,

P₁-P₂ = Drop of pressure

∴ Loss of pressure head = (P₁-P₂)/ ρg

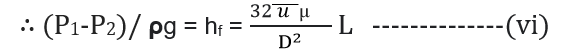
Equation (vi) is called Hagen Poisecuille Formula.