Shear Strength of Soils:
Shear strength of soil is the resistance to deformation by continuous shear displacement of soil particles by the action of shear stresses.
Shear stresses > Shear Strength, failure takes place
- Failure may be sinking of footing or movement of a wedge of soil behind a retaining wall forcing it to move or slide.
- Shear strength is due to friction between particles, interlocking, and cohesion.
- Principal plane – shear stress = 0
- Normal stresses acting on Principal Planes are called Principal Stresses.
- Critical stress values and Obliquities generally occur on major and minor principal planes (two-dimensional solution)
Mohr-Coulomb failure theory:
Coulomb – 1776
Mohr – 1900 (extended Coulomb’s theory)
The theory states that:
- Materials essentially fail in shear. the critical shear stress causing shear failure depends upon the properties of the material as well as normal stress on the failure plane.
- The shear strength is equal to shear stress at failure on a potential plane.
- In a material subjected to three-dimensional principal stress (Ϭ1, Ϭ2, and Ϭ3), the intermediate principal stress Ϭ2 doesn’t have any influence on the strength of the material.
Mathematically,
τ = f(Ϭ)
τ = shear stress
Ϭ= normal stress
MOHR’S STRESS CIRCLE
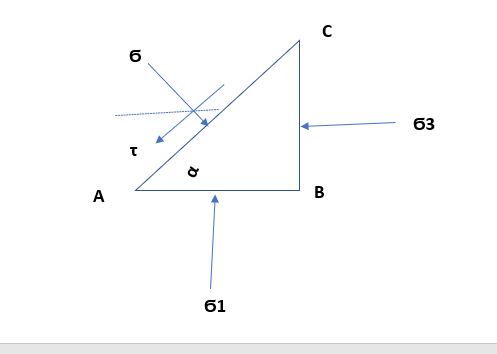
Ϭ – Normal stress
τ -Shear stress
Ϭ1- major principal plane
Ϭ3- minor principal plane
α = Inclination to major plane
Resolving the forces horizontally;
Ϭ3*BC = Ϭ*AC Sinα – τ *AC Cosα
Vertically;
Ϭ1*AB = Ϭ*AC Cosα + τ *AC Sinα
Dividing both sides by AC;
Ϭ3*Sinα = Ϭ*Sinα – τ *Cosα – (i)
And,
Ϭ1*Cosα = Ϭ* Cosα + τ *Sinα- (ii)
Multiplying (i) by Cosα and (ii) by Sinα and subtracting (i) from (ii)
Cosα*Sinα (Ϭ1-Ϭ3) = τ (Sin2α + Cos2α)
Therefore,
τ = {(Ϭ1-Ϭ2)Sinα}/2 – (iii)
Substituting τ in eqn (i)
Ϭ3 Sinα = Ϭ Sinα – {(Ϭ1-Ϭ3)*Sin2α*Cosα}/2
Or, Ϭ3 = Ϭ – {(Ϭ1-Ϭ3)*2Cos2α}/2
Or, Ϭ3 = Ϭ – (Ϭ1-Ϭ3)*Cos2α
Or, Ϭ = Ϭ3 + (Ϭ1-Ϭ3)* Cos2α
Or, Ϭ = Ϭ3 + (Ϭ1-Ϭ3)* {(1+Cos2α)/2}
= Ϭ3 + {(Ϭ1-Ϭ3)/2} + {(Ϭ1-Ϭ3)/2} *Cos2α
Therefore,
Ϭ = {(Ϭ1+Ϭ3)/2} + {(Ϭ1-Ϭ3)/2} *Cos2α – (iv)
MOHR’S CIRCLE

Values of Ϭ, τ for α are plotted, locus of all the points gives a circle known as Mohr Circle
OE – Normal Stress (inclined at α)
ED – Shear Stress (inclined at α)
A – Minor Principal Stress
B – Major Principal Stress
These plane intersects at A (pole)
Principle Planes inclined to the Co-ordinate Axis :
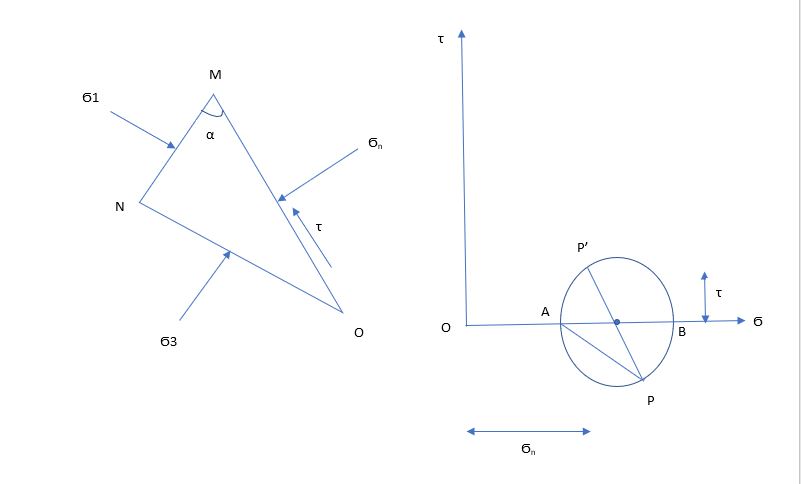
Draw MN//BP (P = Pole) (Major Plane)
Similarly NO//AP (Minor Plane)
OM//P’P (P’ = Pole of inclined Plane)
P’X = τ; OX = Ϭn (for inclined)
Angle of Obliquity:
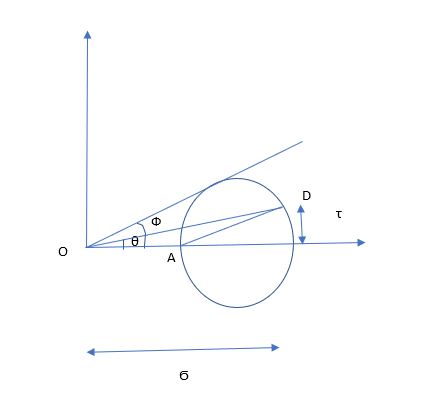
Angle made by resultant to the Plane = θ (angle of Obliquity)
θ= Ф (tangent to circle) (failure envelope)
Ф = internal frictional angle
Relation between Ф and α :
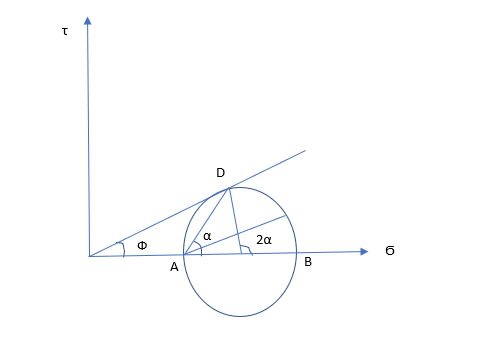
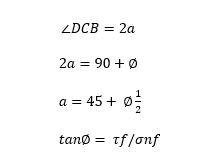
Coulomb failure criterion:
Τf = C + Ϭnf * tanФ (linear function)
Mohr failure criterion :
Τf = f (Ϭnf) (Unique function)
Mohr-Coulomb failure Criterion :
θ= 45 + Ф/2

References:
- Terzaghi, Karl, Peck, R.B & John, Wiley (1969) Soil mechanics in engineering practice, New York.
- Arora , K.R (2008), Soil mechanics and foundation engineering, Delhi: Standard Publisher Distribution

