Numerical Differentiation and Integration

Introduction

Let us consider a set of values (𝑥𝑖, 𝑦𝑖) of a function. The process of computing the derivative or
derivatives of that function at some values of x from the given set of values is called Numerical
Differentiation. This may be done by first approximating the function by suitable interpolation
formula and then differentiating.

Derivatives using Newton’s Forward Difference formula

Newton’s forward interpolation formula

Derivate using Newton’s Backward Difference Formula

Newton’s backward interpolation formula is

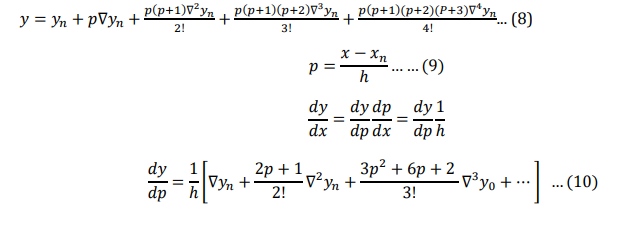
At 𝑥 = 𝑥_𝑛, 𝑝 = 0, hence putting p=0 in equation 10 we get

Note: first derive is also as rate of change, so it can also be asked to find the velocity, second
derivate to find acceleration.

Example: find the first, second and third derivate of 𝑓(𝑥)𝑎𝑡 𝑥 = 1.5 if

𝑥	1.5	2.0	2.5	3.0	3.5	4.0
𝑓(𝑥)	3.375	7.0	13.625	24	38.875	59.0

Solution
We have to find the derivate at the points 𝑥 = 1.5, which is at the beginning of the given data.
Therefore, we use the derivate of Newton’s Forward Interpolation formula.
Forward difference table is

ere 𝑥₀ = 1.5, 𝑦₀ = 3.375, ∆𝑦₀ = 3.625, ∆ ²𝑦₀ = 3, ∆ ³𝑦₀ = 0.75, ∆ ⁴𝑦₀ = 0, ℎ = 0.5

Now using equation for finding the derivate

Example:
The population of a certain town (as obtained from central data) is shown in the following table

Year	1951	1961	1971	1981	1991
population (thousand)	19.36	36.65	58.81	77.21	94.61

Find the rate of growth of the population in the year 1981

Solution
Here we have to find the derivate at 1981 which is near the end of the table, hence we use the
derivative of Newtons Backward difference formula. The table if difference is as follows:

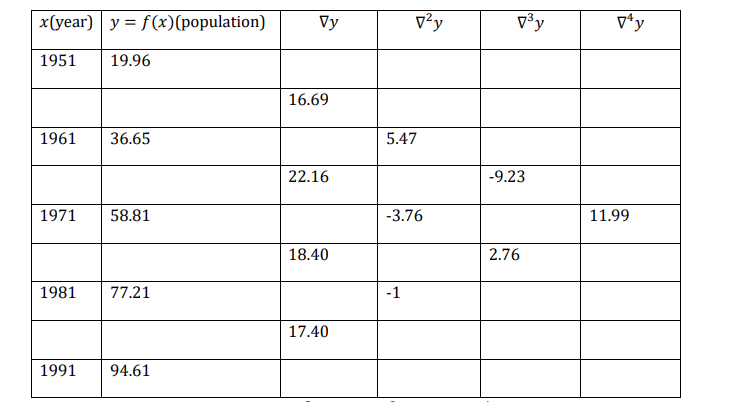
Here ℎ = 10, 𝑥_𝑛 = 1991, ∇𝑦_𝑛 = 17.4, ∇ ²𝑦_𝑛 = −1, ∇ ³𝑦_𝑛 = 2.76, ∇ ⁴𝑦_𝑛= 11.99

We know derivate for backward difference is

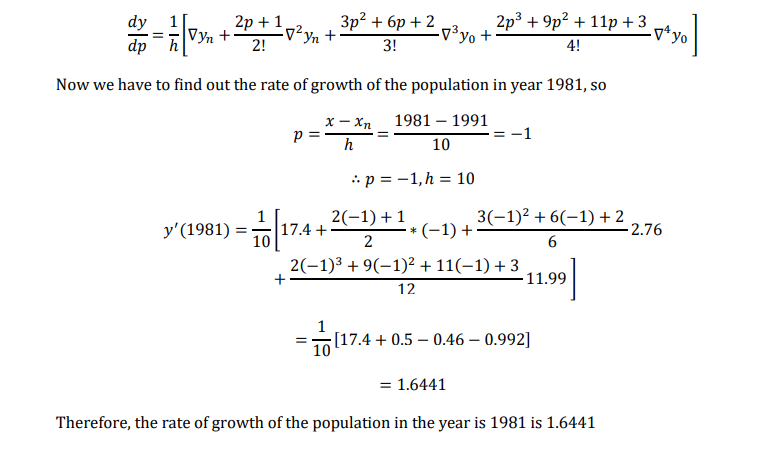
Maxima and minima of tabulated function

We know Newton’s forward interpolation formula as :

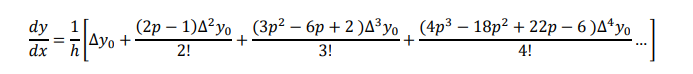
We know that maximum and minimum values of a function 𝑦 = 𝑓(𝑥) can be found by equating 𝑑𝑦/𝑑𝑥 to zero and solution for x

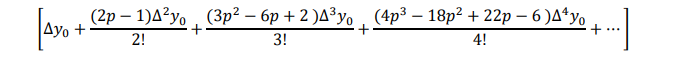
Now for keeping only up to third difference we have

Solving this for p, by substituting ∆𝑦₀, ∆ ²𝑦₀, ∆ ³𝑦₀, we get 𝑥 as 𝑥₀ + 𝑝ℎ at which y is a maximum or minimum

Example: given the following data, find the maximum value of y

𝑥	-1	1	2	3
𝑦	-21	15	12	3

Since the arguments (x -points) aren’t equally spaced we use Newton’s Divided Difference formula

𝑦(𝑥) = 𝑎₀ + 𝑎₁ (𝑥 − 𝑥₀ ) + 𝑎₂ (𝑥 − 𝑥₀ )(𝑥 − 𝑥₁ ) + 𝑎₃ (𝑥 − 𝑥₀ )(𝑥 − 𝑥₁ )(𝑥 − 𝑥₂ )…

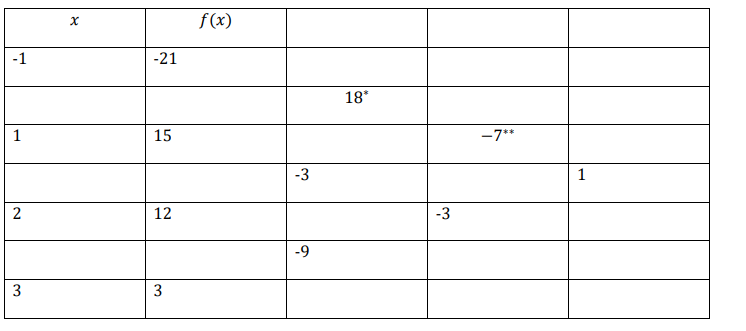
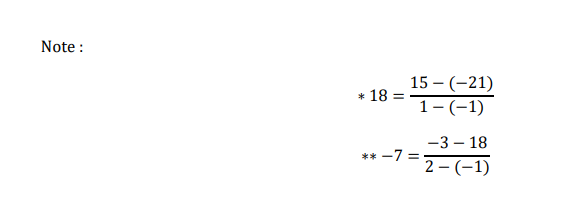
From above table 𝑎₀ = −21, 𝑎₁ = 18, 𝑎₂ = −7, 𝑎₃ = 1,

𝑓(𝑥) = −21 + 18(𝑥 + 1) + (𝑥 + 1)(𝑥 − 1)(−7) + (𝑥 + 1)(𝑥−1)(𝑥 − 2)(1) 𝑓(𝑥) = 𝑥 ³ − 9𝑥 ² + 17𝑥 + 6

For maxima and minima 𝑑𝑦/𝑑𝑥 = 0

3𝑥 ² − 18𝑥 + 17 = 0

On solving we get
𝑥 = 4. .8257 𝑜𝑟 1.1743
Since x=4.8257 is out of range [-1 to 3] , we take x=1.1743

∴ 𝑦𝑚𝑎𝑥 = 𝑥 ³ − 9𝑥 ² + 17𝑥 + 6

= 1.1743³ − 9 ∗ 1.1734² + 17 ∗ 1.1743 + 6

= 15.171612

Differentiating continuous function

If the process of approximating the derivative 𝑓′(𝑥) of the function f(x), when the function itself is
available

Forward Difference Quotient
Consider a small increment ∆𝑥 = ℎ in x, according to Taylor’s theorem, we have

Equation 3 is called first order forward difference quotient. This is also known as two-point formula.
The truncation error is in the order of h and can be decreased by decreasing h.
Similarly, we can show that the first order backward difference quotient is

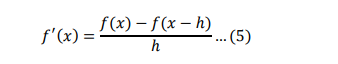
Central Difference Quotient

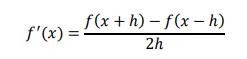
This equation is called second order difference quotient. Note that this is the average of the forward
difference quotient and backward difference equation. This is also called as three-point formula.

Example: estimate approximate derivative of 𝑓(𝑥) = 𝑥 ² 𝑎𝑡 𝑥 = 1, for h=0.2,0.1,0.05 and 0.01, using first order forward difference formula

We know that

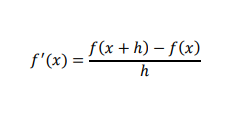
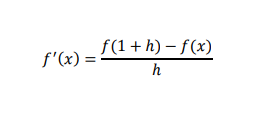
Derivative approximation is tabulated below as:

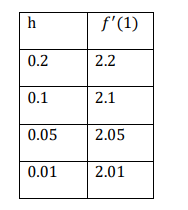
Note that the correct answer is 2. The derivative approximation approaches the exact value as h
decreases.
Now for central difference quotient

Numerical Integration

Newtons Cotes Formula

This is the most popular and widely used in numerical integration.
Numerical integration method uses an interpolating polynomial 𝑝𝑛(𝑥) in place of f(x)

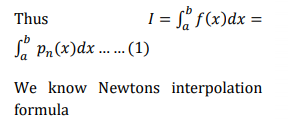
Above equation is known as Newton’s Cote’s quadrature formula, used for numerical integration
If the limits of integration a and b are in the set of interpolating points xi=0,1,2,3…..n, then the formula
is referred as closed form. If the points a and b lie beyond the set of interpolating points, then the
formula is termed as open form. Since the open form formula is not used for definite integration, we
consider here only the closed form methods. They include:

1. Trapezoidal rule
2. Simpson’s 1/3 rule
3. Simpson’s 3/8 rule

Trapezoidal rule (2 point formula)

Putting n=1 in equation 1 and neglecting second and higher order differences we get

Composite Trapezoidal Rule

If the range to be integrated is large, the trapezoidal rule can be improved by dividing the interval
(a,b) into a number of small intervals. The sum
of areas of all the sub-intervals is the integral of
the intervals (a,b) or (x₀,x_n). this is known as
composite trapezoidal rule.

As seen in the figure, there are n+1 equally spaced sampling point that create n segments of equal width h given by

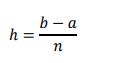
𝑥𝑖 = 𝑎 + 𝑖ℎ 𝑖 = 0,1,2, … n

From the equation of trapezoidal rule,

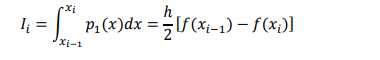
The total area of all the n segments is

Above equation is known as composite trapezoidal rule

Simpson’s 1 ⁄ 3 rule( 3 point formula)

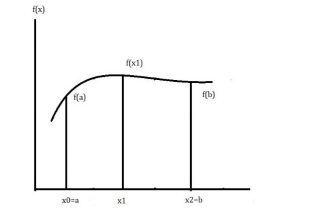
Another popular method is Simpson’s 1/3 rule. Here the function f(x) is approximated by second
order polynomial 𝑝2(𝑥) which passes through three sampling points as shown in figure. The three
points include the end point a & b and midpoint between 𝑥1 = (𝑎 + 𝑏)/2. The width of the segment
h is given by ℎ = (𝑏 − 𝑎)/𝑛 . Take n=2 and neglecting the third and higher order differences we get
(in newton’s cote formula)

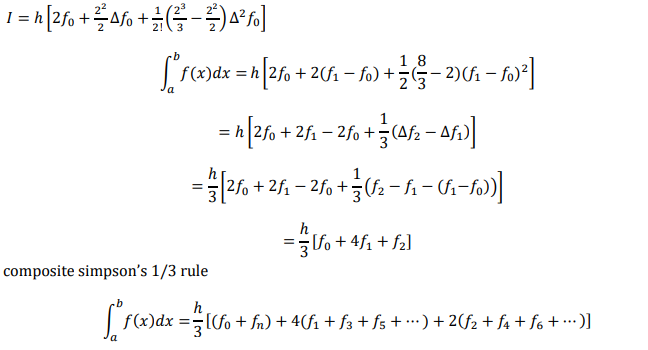
Simpson’s 3/8 rule( 4 point rule)

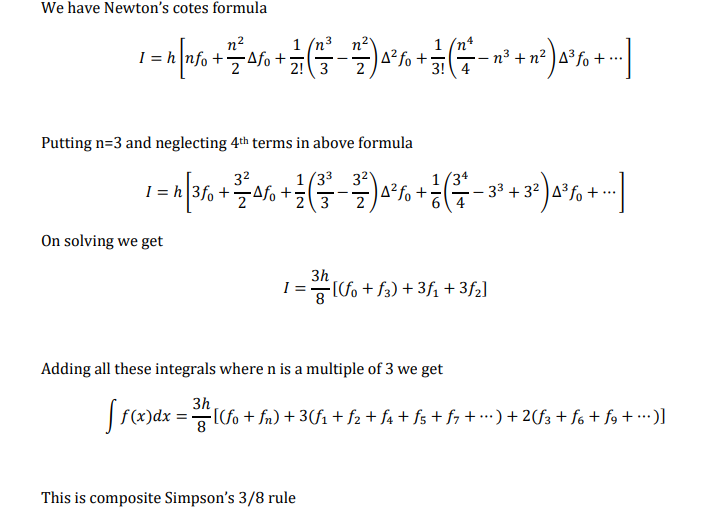
Example:

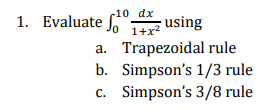
Solution
Taking h=1, divide the whole range of the integration [0,10] into ten equal parts. The value of the integrand for each point of sub division

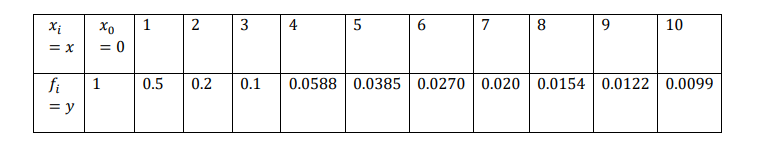
Romberg integration formula/ Richardson’s deferred approach to the limit or Romberg
method

Take an arbitrary value of h and calculate

Gaussian integration

Gaussian integration is based on the concept that the accuracy of numerical integration can be improved by choosing sampling points wisely rather than on the basis of equal sampling. The problem is to compute the values of 𝑥₁& 𝑥₂ given the value of a and b and to choose approximate weights w₁ & w₂ . The method of implementing the strategy of finding approximate values of x_i & w_i and obtaining the integral of f(x) is called Gaussian integration or quadrature. Gaussian integration assumes an approximation of the form

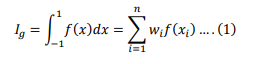
The above equation 1 contains 2n unknowns to be determined. For example for n=2, we need to find the values of w₁,w₂,x₁,x₂. We assume that the integral will be exact up to cubic polynomial. This implies the function x₁,x₂&x₃ can be numerically integrated to obtain exact results.

Assume f(x)=1 (assume the integral is exact up to cubic polynomial)

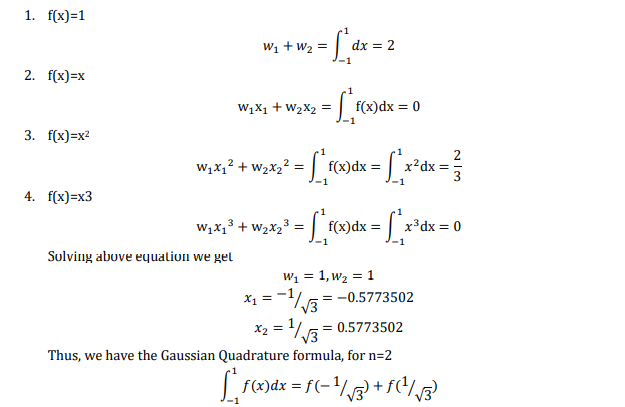
This formula will give correct value for the integral of f(x) in the range (-1,1) for any function
up to third order. The above equation is called gauss Legrendre formula

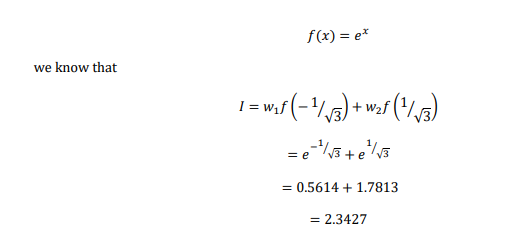
Changing limits of Integration

Note that the Gaussian formula imposed a restriction on the limits of integration to be from -1 to 1.
The restriction can be overcome by using the techniques of the “interval transformation” used in
calculus, let

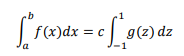
Assume the following transformation between x and new variable z. by following relation.
i.e x=Az+B
this must satisfy the following conditions at x=a, z=-1 & x=b, z=1
i.e B-A=a, A+B=b

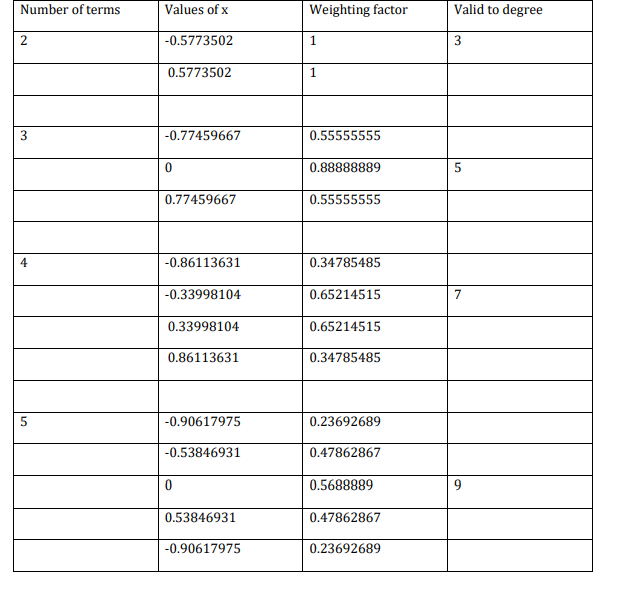
Where w_i and z_i are the weights and quadrature points for the integration domain (-1,1)

Values for gaussian quadrature

Reference 1 : Numerical Methods , Dr. V.N. Vedamurthy & Dr. N. Ch. S. N. Iyengar, Vikas Publishing House.