Probability:
The probability theory provides a means of getting an idea of the likelihood of occurrence of different events resulting from a random experiment in terms of quantitative measures ranging between zero and one. The probability is zero for an impossible event and one for an event which is certain to occur.
Some terminologies:
Random experiment:
An experiment is called a random experiment if outcome of experiment can’t be predicted with certainty ( or result is not unique), but may be any one of the various possible outcomes.
For example, flipping a coin, throwing a balance dice etc. where one cannot predict the outcome of events with certainty.
Sample space:
The set of all possible outcomes of random experiment is sample space. It is denoted by S. For example, while throwing a balance dice, the possible outcomes are 1, 2,3,4,5,6. So sample space is S= {1, 2,3,4,5,6}.
Trial and events:
performing the random experiment is trial and its outcomes are events. For example, flipping a fair coin is a trial where as its outcomes are events.
Simple and Compound Events:
Simple events.
In the simple events we think about the probability of the happening or not-happening of the simple events. Whenever we are tossing the coin we are considering the occurrence of the events of head and tail. In another example, if in a bag there are 10 white balls and 6 red balls and whenever we are trying to find out the probability of drawing a red ball, is included in simple events.
Compound events:
But on the other hand when we consider the joint occurrence of two or more events, it becomes compound events. Unlike simple events here more than one event are taken into consideration.
Equally Likely Events:
Events are said to be equally likely, when there is equal chance of occurring. If one event is not occurred like other events then events are not considered as equally likely. Or in other words events are said to be equally likely when one event does not occur more often than the others.
Mutually Exclusive Events:
The events are said to be mutually exclusive when they are not occurred simultaneously. Among the events, if one event will remain present in a trial other events will not appear. In other words, occurrence of one precludes the occurrence of all the others.
Independent and Dependent Events:
Two or more events are said to be independent when the occurrence of one trial does not affect the other. It indicates the fact that if trial made one by one, one trial is not affected by the other trial. And also one trial never describes anything about the other trials.
Dependent events are those in which the occurrence and non-occurrence of one event in a trial may affect the occurrence of the other trials. Here the events are mutually dependent on each other.
Different Schools of Thought on the Concept of Probability:
There are different schools of thought on the concept of probability:
- Mathematical or prior or classical approach of probability
The definition of probability has been given by a French mathematician named “Laplace”. According to him “ if there are ‘n’ exhaustive, mutually exclusive and equally likely outcomes of an experiment and m of them are favorable to an event A. the probability of happening of event A is denoted by P(A).

This definition was given by James Bernoulli.
Unfavorable no of events for the occurrence of an event A is n-m, so the probability of not happening of an event A is defined as the ratio of n-m/n
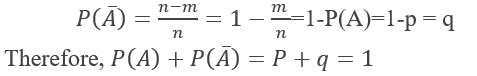
- Statistical or empirical or relative frequency approach:
Suppose that an event A occurs ‘m’ times in ‘n’ repetitions of a random experiment. In the limiting case when n become sufficiently large, it more or less settle to a number which is called probability of happening of an event A.
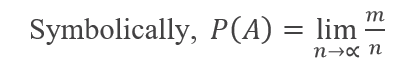
- Axiomatic or modern approach of probability:
Let S be a sample space of random experiment and A be any event in S, then P(.) is probability function define in S and the function P(A) satisfying the following axioms.
i. P(A) ≥ 0, (non- negativity)
ii. P(S) = 1, (total probability)
iii. if A1, A2, ……. An are n mutually exclusive (mutually disjoint) events define in sample space S then,
P (A1UA2U……UAn) = P(A1) + P(A2) +……..+ P(An)
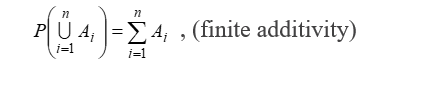
Theorems of probability (or law):
- Additive theorem of Probability.
Statement:
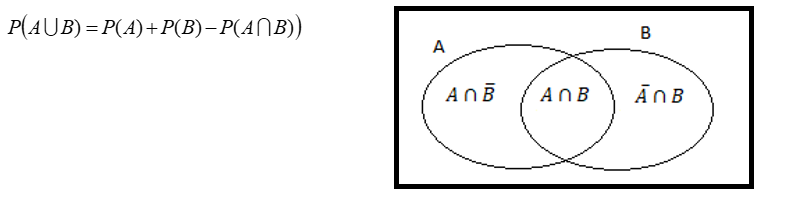
if A and B are two non-mutually exclusive events define in sample space ‘S’ then,
Proof:
Let A and B are two non- mutually exclusive events define in sample space S then from above Venn- diagram we can write,

Note:
If events are mutually exclusive, then an intersection part between events is zero. Then,
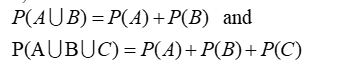
2. Multiplicative theorem of Probability (And law)
Case 1: when events are dependent.
If A and B are dependent events then,
P(A and B) = P(A B) = P(A).P(B/A) ; P(A) > 0 = P(B).P(A/B) ; P(B) > 0
Where P(A/B) and P(B/A) are conditional probabilities of an event A given that, B has been occurred and B given A has been occurred respectively.
Proof:
Suppose sample space contains ‘N’ number of sample points. Out of which number of sample points belongs to the occurrence of an event A, nB number of sample points belongs to the occurrence of an event B and nAB number of sample points belongs to the compound events of A ∩B. Then from the definition of probability we can write,
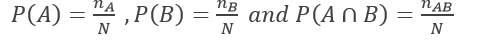
Now, for the conditional probability P(A/B), sample points in the event B acts as sample space for the occurrence of an event A or (A∩B). thus,

| Independence |
Events A and B are said to be independent to each other if the occurrence or non-occurrence of one event doesn’t affect the probability of happening of other event. In other words, if A and B are two independent events, then the probability that they will both occur together is equal to the product of the probability of event A and the probability of event B.
i.e. P (A and B) = P(A∩B) = P(A). P(B)
Thus, if events are independent, then conditional probability becomes unconditional.
i.e. P(A/B) = P(A) and P(B/A) = P(B)
Example:
A coin is tossed three times. Find the probability of getting (i)two heads (ii) no head (iii) at least one head (iv) at most one head (v) head, tail and head in that order.
Solution:
For a fair or unbiased coin P(H)=P(T)=1/2

Example:
In a company, out of 20 candidates 14 men and 6 women apply fort wo vacancies. What is the probability that, i. both men are selected, ii) both women are selected, iii) one man and women are selected in the vacancies.
Solution:
Total no of Candidates(n)= 20
2 candidates can be selected from 20 candidates in 20C2 ways which is exhaustive no. of outcomes, i.e,


Example:
Three groups of children contain 3 boys and 1 girl, 2 boys and 2 girls and 1 boy and 3 girls respectively. One child is selected at random from each group. Show that probability of selecting 1 boy and 2 girls is 13/32.
Solution:

Example:
A Problem of statistics is given to three students A, B and C whose chance of solving it are and respectively. Find the probability that,
- All of them can solve the problem.
- None of them can solve.
- Problem will be solved.
- A and B can solve the problem but C cannot.
- Only one of them can solve.
Solution:


Example:
Past records show that 4 of 135 parts are defective in length, 3 of 141 are defective in width, and 2 of 347 are defective in both. Use these figures to estimate probabilities of the individual events assuming that defects occur independently in length and width.
a) What is the probability that a part produced under the same conditions will be defective in length or width or both?
b) What is the probability that a part will have neither defect?
Solution:
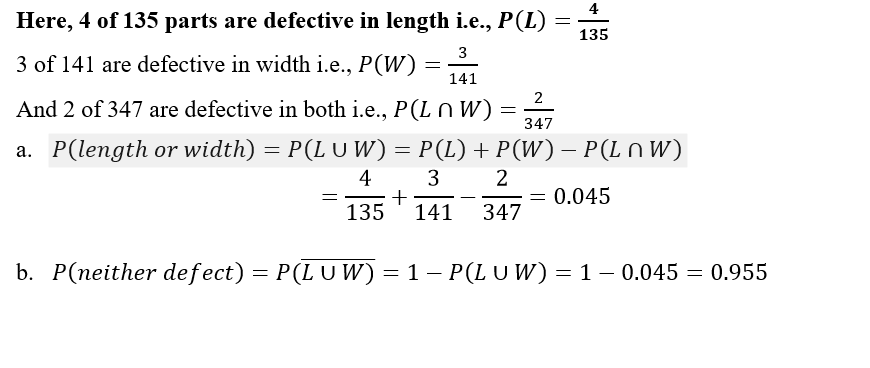
| Conditional probability: |
If A and B are two dependent events, i.e. occurrence of one affects the probability of others and vice versa. Then conditional probability of an event A given that an event B has been already occurred is denoted by P(A/B), and given by,
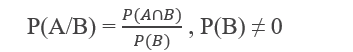
Similarly , conditional probability of an event B given that A has been already occurred is denoted by P(B/A) and given by,
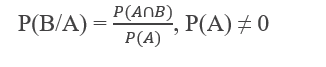
Example:
Suppose that the population of a certain city is 40 percent male and 60 percent female. Suppose also that 50 percent of male and 30 percent of the female smokers. (i) What is the probability that the person selected is male given that it is smoker? (ii) What is the probability that that person selected is female given that she is smoker.
Solution:
For the sake of convenience, let us construct a table from the given information as;
Now,
| Smoker | Non-smoker | Total | |
| Male Female | 20 18 | 20 32 | 40 60 |
| Total | 38 | 52 | 100 |
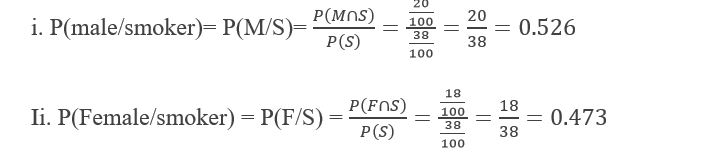
Example:
The probabilities of the monthly snowfall exceeding 10 cm at a particular location in the months of December, January and February are 0.20, 0.40 and 0.60, respectively. For a particular winter:
a) What is the probability of not receiving 10 cm of snowfall in any of the months of December, January and February in a particular winter?
b) What is the probability of receiving at least 10 cm snowfall in a month, in at least two of the three months of that winter?
c) Given that the snowfall exceeded 10 cm in each of only two months, what is the probability that the two months were consecutive?
Solution:
From the given information’s, the probabilities of the monthly snowfall exceeding 10 cm at a particular location in the months of December, January and February are 0.20, 0.40 and 0.60, respectively.

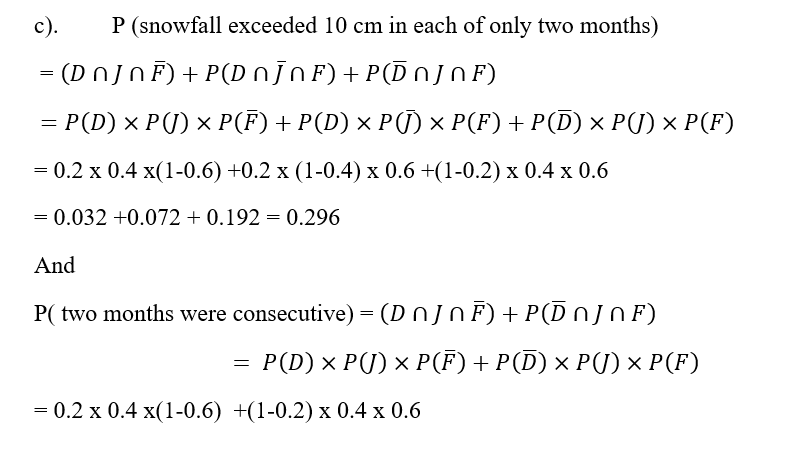

| Baye’s theorem for conditional probability |
Statement:
Let E1, E2 and E3 be mutually exclusive disjoint events of sample space S with P(Ei) ≠ 0, i = 1, 2, 3 then for any arbitrary event say ‘A’ which is subset of ‘S’ such that P(A) > 0, we have
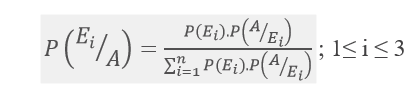
Proof:
Let E1, E2 and E3 are three mutually exclusive events define in sample space ‘S’ and ‘A’ be any arbitrary event. Then relationship between mutually exclusive events and an arbitrary event ‘A’ can be shown in venn-diagram as,
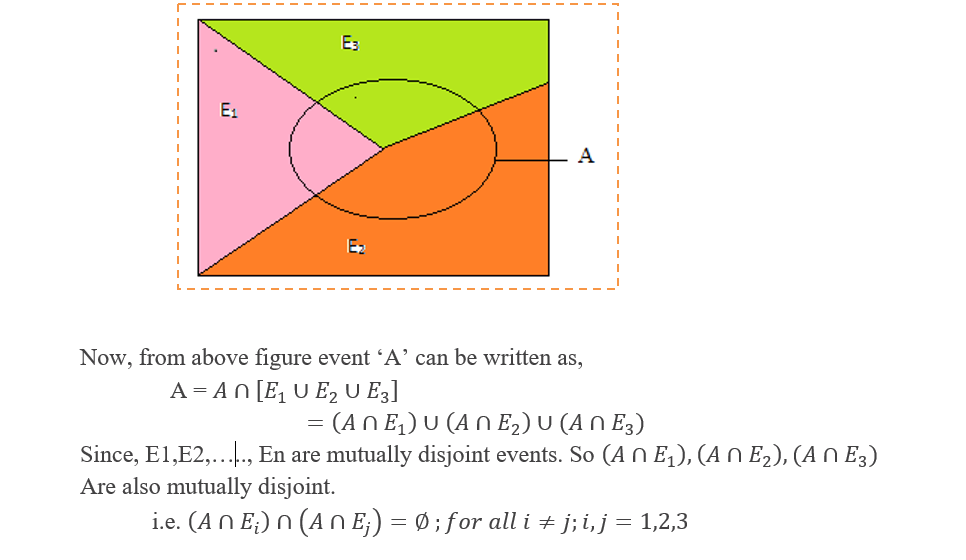

Remarks:
- The probabilities P(E1),P(E2),…….,P(En) are called prior probabilities because they exist before performing the experiment.
- The probabilities P(A/E1), P(A/E2),…..P(A/En) are called likelihood probabilities because that indicate how often A occur for each and every E1,E2,……,En given.
- The probabilities P(Ei/A); i=1,2,3….n are called posteriori probabilities because they are determined after the result of the experiment are known.
Example:
It is known that of the articles produced by a factory, 20% come from Machine A, 30% from Machine B, and 50% from Machine C. The percentages of satisfactory articles among those produced are 95% for A, 85% for B and 90% for C. An article is chosen at random.
a) What is the probability that it is satisfactory?
b) Assuming that the article is satisfactory, what is the probability that it was produced by Machine A?
Solution:
Here from given information’s (Prior probabilities),
20% articles come from machine A; P(A)= 20/100 = 0.20
30% articles come from machine B; P(B) = 30/100 = 0.30
50% articles come from machine C; P(C)= 50/100 = 0.50

Example:
At a particular day of covid-19 pandemics, 2000 frontline works from Kathmandu district are randomly selected and tested for PCR,1500 frontline workers from Bhaktapur and 500 from Lalitpur are randomly selected and tested for PCR. In Kathmandu, Bhaktapur and Lalitpur 25, 7 and 10 are seems to be PCR positive.
1.what is the probability of PCR positive patients?
2. if PCR positive patients are sent in a quarantine and a doctor thoroughly check a PCR positive patient. What is the probability that infected patient is from Kathmandu district?
Solution:

Example:
Box A contains 18 items of which 3 are defective and box B contains 12 non-defectives and 6 defective items. One of the box is selected at random and an item is drawn from it.
1. find the probability that it is defective.
2. if the item is defective, what is the probability that the defective item came from box A?
Solution:
Here, P(selecting box A at random) =P(A) = 1/2= 0.5
And P(selecting Box B at random ) = P(B) = 1/2= 0.5
Let b = defective item
Then likelihood probabilities are ;
P(b/A) = 3/18 and P(b/ B) = 6/18
1. P(defective item) = P(A).P(b/A) + P(B).P(b/B)
= 0.5*3/18 +0.5*6/18
=1/4 =0.25
2. using bayes theorem,
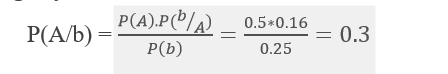
Example:
Three road construction firms, X, Y and Z, bid for a certain contract. From past experience, it is estimated that the probability that X will be awarded the contract is 0.40, while for Y and Z the probabilities are 0.35 and 0.25. If X does receive the contract, the probability that the work will be satisfactorily completed on time is 0.75. For Y and Z these probabilities are 0.80 and 0.70.
i) What is the probability that Y will be awarded the contract and complete the work satisfactorily?
ii) What is the probability that the work will be completed satisfactorily?
iii) It turns out that the work was done satisfactorily. What is the probability that Y was awarded the contract?
Solution:
From given information ,
P(X) = 0.40, P(Y) = 0.35 and P(Z) = 0.25 [ P(X)+P(Y)+P(Z)=1]
Let us define a arbitrary event say (A) then,
A = work will be completed satisfactorily.
Again fron likelihood probabilities,
P(A/X) =0.75, P(B/Y) = 0.80 and P(A/Z) = 0.70
- P(Y will awarded the contract and complete the work satisfactorily) = P(Y∩A)
= P(Y).P(A/Y)
= 0.40 x 0.75
= 0.30
- P( work will be completed satisfactorily)
P(A) = P(X).P(A/X) + P(Y).P(A/Y) + P(Z).P(A/Z)
= 0.40×0.75 + 0.35×0.80 + 0.25×0.70
= 0.755
- Now using Bayes theorem,
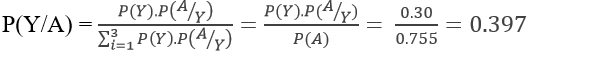
Reference : Probability and statistics for engineers by Toya Naryan Paudel & Pradeep Kunwar, Sukunda Pustak Bhawan.

